题目内容
已知点C,D在线段AB上.
(1)若线段AB,CD的长度满足(6-3CD)2+|
AB-5|=0,求线段AB,CD的长度;
(2)在(1)的条件下,若M,N分别是AD,BC的中点,且2<AC<6,求线段MN的长度;
(3)若C,D是线段AB的三等分线,P是线段AC上任意一点,求
.
(1)若线段AB,CD的长度满足(6-3CD)2+|
| 1 |
| 2 |
(2)在(1)的条件下,若M,N分别是AD,BC的中点,且2<AC<6,求线段MN的长度;
(3)若C,D是线段AB的三等分线,P是线段AC上任意一点,求
| 2PB-PA |
| PD |
考点:两点间的距离
专题:
分析:(1)根据非负数的性质可求线段AB,CD的长度;
(2)画出图形,根据中点的定义得到MD+NC=MN+CD=
AD+
BC=
(AD+BC)=
(AB+CD),代入数据即可求解;
(3)根据线段三等分线的定义将
变形为
,再约分即可求解.
(2)画出图形,根据中点的定义得到MD+NC=MN+CD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)根据线段三等分线的定义将
| 2PB-PA |
| PD |
| 2(AB-PA)-PA | ||
|
解答:解:(1)线段AB,CD的长度满足(6-3CD)2+|
AB-5|=0,
∴6-3CD=0,
AB-5=0,
解得CD=2,AB=10.
故线段AB的长度是10,线段CD的长度是2;
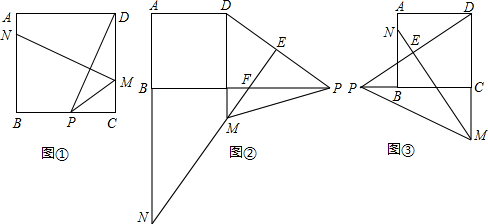
(2)如图,

∵M,N分别是AD,BC的中点,
∴MD=
AD,NC=
BC,
∴MD+NC=MN+CD=
AD+
BC=
(AD+BC)=
(AB+CD),
∴MN+2=
×(10+2),
解得MN=4.
线段MN的长度是4;
(3)如图:

∵C,D是线段AB的三等分线,
∴
=
=
=3.
| 1 |
| 2 |
∴6-3CD=0,
| 1 |
| 2 |
解得CD=2,AB=10.
故线段AB的长度是10,线段CD的长度是2;
(2)如图,

∵M,N分别是AD,BC的中点,
∴MD=
| 1 |
| 2 |
| 1 |
| 2 |
∴MD+NC=MN+CD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴MN+2=
| 1 |
| 2 |
解得MN=4.
线段MN的长度是4;
(3)如图:

∵C,D是线段AB的三等分线,
∴
| 2PB-PA |
| PD |
| 2(AB-PA)-PA | ||
|
| 2AB-3PA | ||
|
点评:考查了两点间的距离,非负数的性质,中点的定义,以及线段三等分线的定义,综合性较强,有一定的难度.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
如果线段AB=3cm,BC=1cm,那么A、C两点的距离d的长度为( )
| A、4cm |
| B、2cm |
| C、4cm或2cm |
| D、小于或等于4cm,且大于或等于2cm |
 如图,∠ACB=90°,CD⊥AB于D.则:
如图,∠ACB=90°,CD⊥AB于D.则: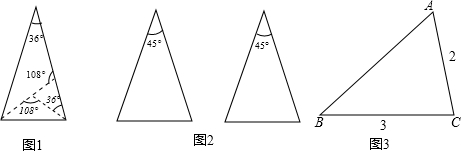
 在圆O中,∠ACB=∠BCA=60°,AC=2
在圆O中,∠ACB=∠BCA=60°,AC=2 如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,求∠EDF的度数.
如图,在△ABC中,内切圆I和边BC、CA、AB分别相切于点D、E、F,若∠B=60°,∠C=70°,求∠EDF的度数. 如图,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行.
如图,∠1=∠2=115°,∠3=65°,图中有哪些直线互相平行.