题目内容
 CE是△ABC的外角∠ACD的平分线,AB的垂直平分线FG分别交AB,CE于F,G.联结GA,GB.求证:∠GAC=∠GBC.
CE是△ABC的外角∠ACD的平分线,AB的垂直平分线FG分别交AB,CE于F,G.联结GA,GB.求证:∠GAC=∠GBC.考点:全等三角形的判定与性质,角平分线的性质
专题:证明题
分析:过G作GH⊥CD,GQ⊥AC,根据垂直平分线和角平分线的性质可得GA=GB,GQ=GH即可证明RT△AGQ≌RT△BGH,即可解题.
解答:证明:过G作GH⊥CD,GQ⊥AC,

∵CE是∠ACD平分线,
∴GQ=GH,
∵FG是AB垂直平分线,
∴AG=BG,
∵在RT△AGQ和RT△BGH中,
,
∴RT△AGQ≌RT△BGH,(HL)
∴∠GAC=∠GBC.

∵CE是∠ACD平分线,
∴GQ=GH,
∵FG是AB垂直平分线,
∴AG=BG,
∵在RT△AGQ和RT△BGH中,
|
∴RT△AGQ≌RT△BGH,(HL)
∴∠GAC=∠GBC.
点评:本题考查了全等三角形的判定,考查了全等三角形对应角相等的性质,本题中求证RT△AGQ≌RT△BGH是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
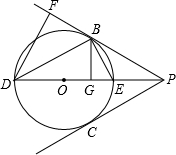 如图,PB、PC分别切⊙O于B、C,DE是圆的直径.
如图,PB、PC分别切⊙O于B、C,DE是圆的直径.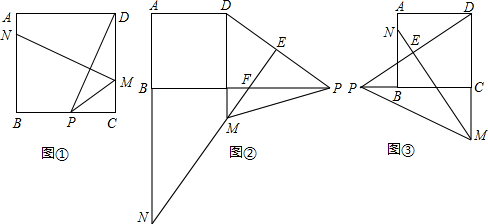
 如图所示,分别是小红和小华的花手帕(都是正方形)
如图所示,分别是小红和小华的花手帕(都是正方形)