题目内容
8.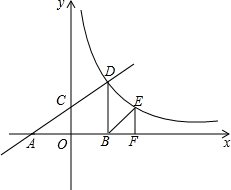 如图,直线y=$\frac{1}{2}$x+2分别交x轴、y轴于点A,C,与反比例函数的图象在第一象限内相交于点D,过点D作DB⊥x轴于点B,若0B=2.
如图,直线y=$\frac{1}{2}$x+2分别交x轴、y轴于点A,C,与反比例函数的图象在第一象限内相交于点D,过点D作DB⊥x轴于点B,若0B=2.(1)求这个反比例函数的表达式;
(2)设点E在已知反比例函数的图象上,且点E在直线DB的右侧,作EF⊥x轴于点F,是否存在点E使得△BEF与△AOC相似?若存在.求点E的坐标;若不存在,说明理由.
分析 (1)首先得出D点横坐标,进而代入一次函数解析式即可得出D点坐标,即可得出反比例函数解析式;
(2)分别利用当△EBF∽△ACO时,以及当△EBF∽△CAO时,表示出E点坐标,进而求出答案.
解答 解:(1)∵OB=2,
∴D点横坐标为:2,
x=2时,y=$\frac{1}{2}$×2+2=3,
∴D(2,3),故xy=6,
∴这个反比例函数的表达式为:y=$\frac{6}{x}$;
(2)∵直线y=$\frac{1}{2}$x+2分别交x轴、y轴于点A,C,
∴y=0时,0=$\frac{1}{2}$x+2,解得:x=-4,当x=0时,y=2,
∴CO=2,AO=-4,
当△EBF∽△ACO时,$\frac{EF}{BF}$=$\frac{AO}{CO}$=2,
设BF=m,则EF=2m,E(2+m,2m),
代入y=$\frac{6}{x}$得,m1=-3(舍),m2=1,E(3,2).
当△EBF∽△CAO时,
同理得:BF=2EF,设EF=n,BF=2n,得:E(2+2n,n),
代入y=$\frac{6}{x}$得:n=$\frac{-1±\sqrt{13}}{2}$(舍去负值),
则2+2n=$\sqrt{13}$+1,
故E($\sqrt{13}$+1,$\frac{-1+\sqrt{13}}{2}$),
综上所述:E点坐标为:(3,2),($\sqrt{13}$+1,$\frac{-1+\sqrt{13}}{2}$).
点评 本题考查了反比例函数综合以及相似三角形的判定与性质等相关知识,利用分类讨论得出符合题意的E点坐标是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目