题目内容
19.半径为2cm的圆的内接正三、四、六边形的边长分别为a3=2$\sqrt{3}$cm,a4=2$\sqrt{2}$cm,a5=2cm.分析 正三角形的计算可以过中心作一边的垂线,然后连接中心与这边的端点,即可得到一个直角三角形,解直角三角形即可;
正方形的边以及对应的两条半径正好构成等腰直角三角形,根据勾股定理即可求解;
正六边形的边长与半径相等即可求解.
解答 解:正三角形的中心角是$\frac{1}{3}$×360°=120°,
则边长是:2×2sin60°=2$\sqrt{3}$cm;
正方形的边长是:2$\sqrt{2}$cm;
正六边形的边长等于半径,因而边长是2cm.
故答案是:2$\sqrt{3}$cm,2$\sqrt{2}$cm,2cm.
点评 本题考查了正多边形和圆,正多边形的计算的基本思路是转化为直角三角形的计算.

练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案
相关题目
4.某班女生有n人,男生人数是女生人数的$\frac{3}{2}$,则全班人数是( )
| A. | $\frac{3}{2}$n | B. | $\frac{2}{3}$n | C. | $\frac{5}{2}$n | D. | $\frac{2}{5}$n |
11.直角三角形的面积为4$\sqrt{3}$,两直角边的比是2:$\sqrt{3}$,则它的斜边长为( )
| A. | 2 | B. | 4 | C. | 2$\sqrt{3}$ | D. | 2$\sqrt{7}$ |
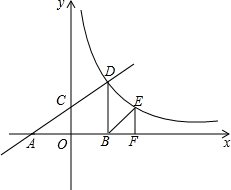 如图,直线y=$\frac{1}{2}$x+2分别交x轴、y轴于点A,C,与反比例函数的图象在第一象限内相交于点D,过点D作DB⊥x轴于点B,若0B=2.
如图,直线y=$\frac{1}{2}$x+2分别交x轴、y轴于点A,C,与反比例函数的图象在第一象限内相交于点D,过点D作DB⊥x轴于点B,若0B=2.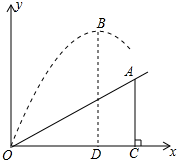 如图,小明在一次高尔夫球争霸赛中从山坡上的点O打出一球向球洞A飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度12m时,球移动的水平距离为9m.已知山坡OA与水平方向OC的夹角为30°,O,A两点相距8$\sqrt{3}$ m.
如图,小明在一次高尔夫球争霸赛中从山坡上的点O打出一球向球洞A飞去,球的飞行路线为抛物线,如果不考虑空气阻力,当球达到最大铅垂高度12m时,球移动的水平距离为9m.已知山坡OA与水平方向OC的夹角为30°,O,A两点相距8$\sqrt{3}$ m.