题目内容
8.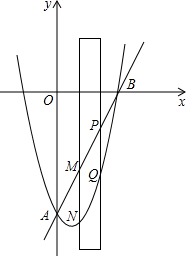 如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).
如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).(1)求抛物线的函数解析式.
(2)当m为何值时,以M、N、P、Q为顶点的四边形是平行四边形?请说明理由;
(3)在抛物线上的对称轴上是否存在点D使得点D到直线AB和到x轴的距离相等?若存在,请直接写出点D的坐标;若不存在,请说明理由.
分析 (1)先利用一次函数图象上点的坐标特征求出A点和B点坐标,然后把A点和B点坐标代入y=x2+bx+c得关于b、c的方程组,再解方程组求出b、c即可得到抛物线解析式;
(2)作PH⊥MN于H,如图1,证明△PHM∽△BOA,利用相似比得到PH:HM=1:2,则可设PH=x,HM=2x,利用勾股定理计算出PM=$\sqrt{5}$x,所以$\sqrt{5}$x=$\sqrt{5}$,解得x=1,再设M(m,2m-8),则P(m+1,2m-6),接着表示出N(m,m2-2m-8),Q[m+1,(m+1)2-2(m+1)-8],根据平行线四边形的判定方法当MN=PQ时,以M、N、P、Q为顶点的四边形是平行四边形,即|m2-2m-8-(2m-8)|=|(m+1)2-2(m+1)-8-(2m-6)|,然后解绝对值方程求出m即可得到满足条件的m的值;
(3)先确定抛物线的对称轴为直线x=1,作AC垂直对称轴于C,对称轴交x轴于E,DF⊥AB于F,AB与对称轴交于点K,如图2,则K(1,-6),C(1,-8),利用勾股定理可计算出AK=$\sqrt{5}$,设D(1,t),则DE=DF=|t|,通过证明△DKF∽△AKC,利用相似比得到|t|:1=(t+6):$\sqrt{5}$,然后解方程求出t即可得到D点坐标.
解答 解:(1)当x=0时,y=2x-8=-8,则A(0,-8),
当y=0时,2x-8=0,解得x=4,则B(4,0),
把A(0,-8),B(4,0)代入y=x2+bx+c得$\left\{\begin{array}{l}{c=-8}\\{16+4b+c=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=-2}\\{c=-8}\end{array}\right.$,
所以抛物线解析式为y=x2-2x-8;
(2)作PH⊥MN于H,如图1 ,
,
∵HM∥OA,
∴∠OAB=∠HMP,
∴△PHM∽△BOA,
∴PH:OB=HM:OA,即PH:4=HM:8,
∴PH:HM=1:2,
设PH=x,则HM=2x,
在Rt△PHM中,PM=$\sqrt{{x}^{2}+(2x)^{2}}$=$\sqrt{5}$x,
∴$\sqrt{5}$x=$\sqrt{5}$,解得x=1,即PH=1,HM=2,
设M(m,2m-8),则P(m+1,2m-6),
∴N(m,m2-2m-8),Q[m+1,(m+1)2-2(m+1)-8],
∵MN∥PQ,
∴当MN=PQ时,以M、N、P、Q为顶点的四边形是平行四边形,
即|m2-2m-8-(2m-8)|=|(m+1)2-2(m+1)-8-(2m-6)|,
解得m=$\frac{3}{2}$或m=$\frac{3±\sqrt{15}}{2}$,
而0<m<4,
∴当m为$\frac{3}{2}$或$\frac{3+\sqrt{15}}{2}$时,以M、N、P、Q为顶点的四边形是平行四边形;
(3)存在.
抛物线的对称轴为直线x=-$\frac{-2}{2×1}$=1,
作AC垂直对称轴于C,对称轴交x轴于E,DF⊥AB于F,AB与对称轴交于点K,如图2,
当x=1时,y=2x-8=-6,则K(1,-6),而C(1,-8),
在Rt△ACK中,AK=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
设D(1,t),则DE=DF=|t|,
∵∠DKF=∠AKC,
∴△DKF∽△AKC,
∴DF:AC=DK:AK,即|t|:1=(t+6):$\sqrt{5}$,
解得t=$\frac{3-3\sqrt{5}}{2}$或t=$\frac{3+3\sqrt{5}}{2}$,
∴D点坐标为(1,$\frac{3-3\sqrt{5}}{2}$)或(1,$\frac{3+3\sqrt{5}}{2}$).
点评 本题考查了二次函数的综合题:熟练掌握二次函数图象上点的坐标特征、二次函数的性质和平行四边形的判定方法;会利用待定系数法求二次函数解析式;理解坐标与图形性质;能运用相似比计算线段的长或表示线段之间的关系.

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
| A. | x1<x2<x3 | B. | x1<x3<x2 | C. | x2<x1<x3 | D. | x2<x3<x1 |
| A. | -1 | B. | $-\frac{1}{2}$ | C. | 0 | D. | 1 |
 如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )
如图,△ABC中,AB的垂直平分线交AC于点M,若CM=3cm,BC=5cm,AM=7cm,则△MBC的周长为( )| A. | 12cm | B. | 9cm | C. | 7cm | D. | 15cm |
 黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).
黔东南州某校吴老师组织九(1)班同学开展数学活动,带领同学们测量学校附近一电线杆的高.已知电线杆直立于地面上,某天在太阳光的照射下,电线杆的影子(折线BCD)恰好落在水平地面和斜坡上,在D处测得电线杆顶端A的仰角为30°,在C处测得电线杆顶端A得仰角为45°,斜坡与地面成60°角,CD=4m,请你根据这些数据求电线杆的高(AB).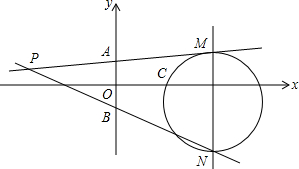 如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.