题目内容
3．在一个不透明的口袋里装有四个小球，四个小球上分别标有数字：1、3、5、7，它们除了所标数字不同之外，没有其它区别．（1）随机地从口袋里抽取一个小球，求取出的小球上的数字为5的概率；
（2）若小刚先随机地从口袋里抽取一个小球后，小丽再从剩余的三个球中随机地抽取一个小球．以小刚取出的小球上所标的数作为等腰三角形的腰，以小丽取出的小球上所标的数作为等腰三角形的底．请你用画树状图或列表的方法表示所有等可能的结果，并求出能构成等腰三角形的概率．
分析 （1）由概率公式容易得出结果；
（2）画出树状图，所有等可能结果共有12种，其中能构成等腰三角形有8种，即可求出概率．
解答 解：（1）P（取出的小球上的数字为5）=$\frac{1}{4}$；
（2）画出树状图如下
所有等可能结果共有12种，其中能构成等腰三角形有8种，
∴P（能构成等腰三角形）=$\frac{8}{12}$=$\frac{2}{3}$．
点评 本题考查的是用列表法或画树状图法求概率、概率公式、等腰三角形的判定与性质．列表法或画树状图法可以不重复不遗漏的列出所有可能的结果，适合于两步完成的事件．
练习册系列答案
相关题目
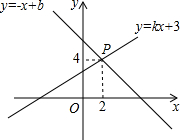如图，已知一次函数y=kx+3和y=-x+b的图象交于点P（2，4），则关于x的方程kx+3=-x+b的解是x=2．
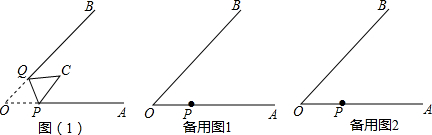
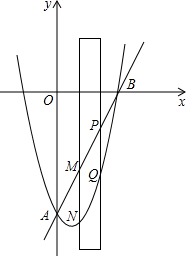如图，抛物线与直线y=2x-8交于A，B两点，有一直尺平行于y轴移动，直尺两长边所在直线AB和抛物线截得两线段NM、PQ，点P、M在直线AB上且PM=$\sqrt{5}$，设M点的横坐标为m（0＜m＜4）．
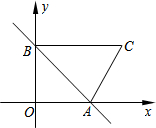已知一次函数y=-x+3的图象与x轴交于点A、与y轴交于点B，BC∥x轴，且∠ACB的正切值为3．