题目内容
18.解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,把解集在数轴上表示出来,并写出符合不等式组的所有整数解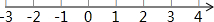
分析 首先解每个不等式,把解集在数轴上表示出来即可得到不等式组的解集,然后确定解集中的整数即可.
解答 解:$\left\{\begin{array}{l}{4x>2x-6…①}\\{\frac{x-1}{3}≤\frac{x+1}{9}…②}\end{array}\right.$,
解①得x>-3,
解②得x≤2.
不等式组的解集是-3<x≤2.
则整数解释-2,-1,0,1,2.
点评 本题考查了一元一次不等式组的解法:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.方法与步骤:①求不等式组中每个不等式的解集;②利用数轴求公共部分.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
3.用反证法证明真命题“四边形中至少有一个角不小于90°”时,应假设( )
| A. | 四边形中没有一个角不小于90° | B. | 四边形中至少有两个角不小于90° | ||
| C. | 四边形中四个角都不小于90° | D. | 四边形中至多有一个角不小于90° |
7. 如图,同位角是( )
如图,同位角是( )
 如图,同位角是( )
如图,同位角是( )| A. | ∠1和∠2 | B. | ∠3和∠4 | C. | ∠2和∠4 | D. | ∠1和∠4 |
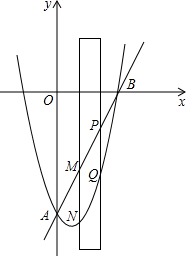 如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).
如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).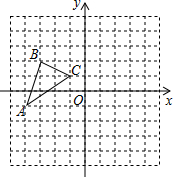 如图所示,在平面直角坐标系中,平移三角形ABC,使A的对应点A1的坐标为(1,-3),B的对应点为B1,C的对应点为C1.
如图所示,在平面直角坐标系中,平移三角形ABC,使A的对应点A1的坐标为(1,-3),B的对应点为B1,C的对应点为C1.