题目内容
18.下列二次根式中,最简二次根式是( )| A. | $\sqrt{\frac{1}{3}}$ | B. | $\sqrt{0.3}$ | C. | $\sqrt{3}$ | D. | $\sqrt{20}$ |
分析 判定一个二次根式是不是最简二次根式的方法,就是逐个检查最简二次根式的两个条件是否同时满足,同时满足的就是最简二次根式,否则就不是.
解答 解:A、$\sqrt{\frac{1}{3}}=\frac{\sqrt{3}}{3}$,被开方数含分母,不是最简二次根式;
B、$\sqrt{0.3}=\sqrt{\frac{3}{10}}=\frac{\sqrt{30}}{10}$,被开方数含分母,不是最简二次根式;
C、$\sqrt{3}$,是最简二次根式;
D、$\sqrt{20}=2\sqrt{5}$,被开方数含能开得尽方的因数,不是最简二次根式;
故选:C.
点评 本题考查最简二次根式的定义,最简二次根式必须满足两个条件:(1)被开方数不含分母;(2)被开方数不含能开得尽方的因数或因式.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.已知正比例函数y=kx的图象与反比例函数y=$\frac{m}{x}$的图象交于A,B两点,若点A的坐标为(-2,1),则关于x的方程$\frac{m}{x}$=kx的两个实数根分别为( )
| A. | x1=-1,x2=1 | B. | x1=-1,x2=2 | C. | x1=-2,x2=1 | D. | x1=-2,x2=2 |

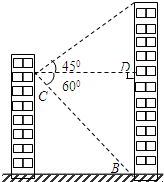 小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为45°,大厦底部B的俯角为60°.求小明家所在居民楼与大厦的距离CD的长度.计算结果保留根号.
小明家所在居民楼的对面有一座大厦AB,AB=80米.为测量这座居民楼与大厦之间的距离,小明从自己家的窗户C处测得大厦顶部A的仰角为45°,大厦底部B的俯角为60°.求小明家所在居民楼与大厦的距离CD的长度.计算结果保留根号.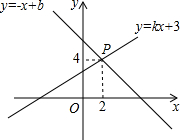 如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的方程kx+3=-x+b的解是x=2.
如图,已知一次函数y=kx+3和y=-x+b的图象交于点P(2,4),则关于x的方程kx+3=-x+b的解是x=2.

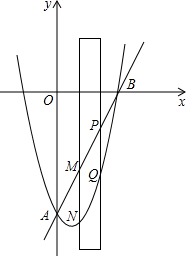 如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).
如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).