题目内容
17.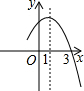 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0; ②方程ax2+bx+c=0的根是x1=-1,x2=3
③a+b+c>0 ④当x>1时,y随x的增大而增大.
正确的说法有①②③.
分析 由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解答 解:∵抛物线的开口向下,
∴a<0,
∵与y轴的交点为在y轴的正半轴上,
∴c>0,
∴ac<0,故①正确;
∵对称轴为x=1,抛物线与x轴的一个交点为(3,0),
∴另一个交点为(-1,0),
∴方程ax2+bx+c=0的根是x1=-1,x2=3,
故②正确;
当x=1时,y=a+b+c>0,
故③正确;
∴a、b异号,即b<0,
当x>1时,y随x的增大而减小,故④错误.
∴其中正确的说法有①②③;
故答案为:①②③.
点评 此题考查了二次函数的图象与系数的关系,二次函数y=ax2+bx+c系数符号的确定:(1)a由抛物线开口方向确定:开口方向向上,则a>0;否则a<0.(2)c由抛物线与y轴的交点确定:交点在y轴正半轴,则c>0;否则c<0.(3)当x=1时,可确定a+b+c的符号,当x=-1时,可确定a-b+c的符号.

练习册系列答案
相关题目
2.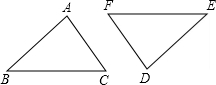 如图,△ABC 和△DEF中,已有条件AB=DE,还要添加两个条件才能使△ABC≌△DEF,不能添加的一组是( )
如图,△ABC 和△DEF中,已有条件AB=DE,还要添加两个条件才能使△ABC≌△DEF,不能添加的一组是( )
 如图,△ABC 和△DEF中,已有条件AB=DE,还要添加两个条件才能使△ABC≌△DEF,不能添加的一组是( )
如图,△ABC 和△DEF中,已有条件AB=DE,还要添加两个条件才能使△ABC≌△DEF,不能添加的一组是( )| A. | ∠B=∠E,BC=EF | B. | ∠A=∠D,∠B=∠E | C. | ∠A=∠D,BC=EF | D. | BC=EF,AC=DF |
6.在平面直角坐标系中,以点A(-1,0)为圆心,$\sqrt{2}$为半径画圆,若B为圆上任意一点,d为点B到x轴的距离,则下列关于d的说法中,正确的是( )
| A. | 有最大值2 | B. | 有最大值$\sqrt{2}$,但没有最小值 | ||
| C. | 没有最大值,但有最小值0 | D. | 既有最大值$\sqrt{2}$,又有最小值0 |
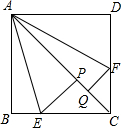 如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.
如图,在正方形ABCD内,以A为顶点作∠EAF=45°.设这个角的两边分别交正方形的边BC、CD于E、F,自E、F分别作正方形AC的垂线,垂足为P、Q.求证:过B、P、Q所作的圆的圆心在BC上.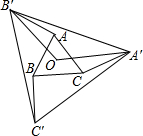 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、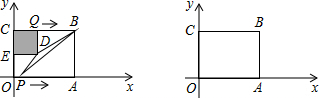
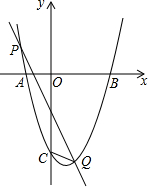 已知:抛物线y=x2+bx+c的对称轴x=1,与x轴交于A,B两点,且A(-1,0).与y轴交于点C,直线y=kx-1与抛物线交于P、Q两点且y轴平分△CPQ的面积.求k的值.
已知:抛物线y=x2+bx+c的对称轴x=1,与x轴交于A,B两点,且A(-1,0).与y轴交于点C,直线y=kx-1与抛物线交于P、Q两点且y轴平分△CPQ的面积.求k的值.