题目内容
12.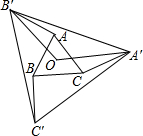 如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、
如图,O是边长为1的等边△ABC的中心,将AB、BC、CA分别绕点A、点B、点C顺时针旋转α(0°<α<180°),得到AB'、BC'、CA',连接A'B'、B'C'、A'C'、OA'、OB'.当α=150°时,△A'B'C'的周长最大,最大值为$\frac{3}{2}$+$\frac{3}{2}$$\sqrt{3}$..
分析 如图,连接OA、OB、OC、OC′.由△OAB′≌△OCA′,推出∠A′OB′=∠A′OC′=∠B′OC′=120°,△A′B′C′是等边三角形,当O、C、A′共线时,OA′=OC+CA′=OC+CA=$\frac{\sqrt{3}}{3}$+1时,OA′最长,此时△A′B′C′的最长最大.
解答 解:如图,连接OA、OB、OC、OC′.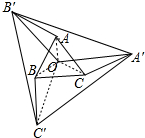
∵O是等边三角形△ABC是中心,
∴∠BAO=∠ACO=30°,OA=OC,
,∵∠BAB′=∠ACA′=α,
∴∠OAB′=∠OCA′,
在△OAB′和△OCA′中,
$\left\{\begin{array}{l}{OA=OC}\\{∠OAB′=∠OCA′}\\{AB′=CA′}\end{array}\right.$,
∴△OAB′≌△OCA′,
∴∠AOB′=∠COA′,OA′=OB′
∴∠A′OB′=∠AOC=120°,同理可证∠A′OC′=∠C′OB′=120°,OA′=OC′
则有△A′OB′≌△A′OC′≌△C′OB′,
∴A′B′=A′C′=B′C′,
在△A′OB′中,∵∠A′OB′=120°,OB′=OA′,
∴当OA′最长时,A′B′最长,
∵OA′≤OC+CA′,
∴当O、C、A′共线时,OA′=OC+CA′=OC+CA=$\frac{\sqrt{3}}{3}$+1时,OA′最长,
此时A′B′=$\frac{\sqrt{3}}{2}$•($\frac{\sqrt{3}}{3}$+1)=$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$,α=150°,
∴△A′B′C′的最长的最大值为$\frac{3}{2}$+$\frac{3\sqrt{3}}{2}$.
故答案为150,$\frac{3}{2}$+$\frac{3}{2}$$\sqrt{3}$.
点评 本题考查旋转变换、等边三角形的性质和判定、全等三角形的判定和性质、最大值问题等知识,解题的关键是灵活应用全等三角形的判定,学会利用三角形的三边关系解决最大值问题,属于中考常考题型.

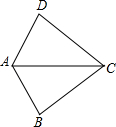 如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | AB=AD | B. | ∠BCA=∠DCA | C. | CB=CD | D. | ∠ADC=∠ABC |
| A. | 将l1沿y轴向下平移2个单位 | B. | 将l1沿y轴向下平移4个单位 | ||
| C. | 将l1沿x轴向右平移2个单位 | D. | 将l1沿x轴向左平移2个单位 |
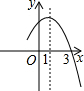 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0; ②方程ax2+bx+c=0的根是x1=-1,x2=3
③a+b+c>0 ④当x>1时,y随x的增大而增大.
正确的说法有①②③.
| A. | x2-1=x | B. | $\frac{1}{x}$+2=x | C. | 3x+$\frac{1}{2}$=$\frac{5-x}{3}$ | D. | 2x-y=1 |
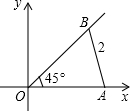 在平面直角坐标系xOy中,点A是x轴正半轴上任意一点,点B是第一象限角平分线上一点(不含原点),AB=2,∠AOB=45°,以AB为一边作正△ABC,则
在平面直角坐标系xOy中,点A是x轴正半轴上任意一点,点B是第一象限角平分线上一点(不含原点),AB=2,∠AOB=45°,以AB为一边作正△ABC,则