题目内容
9.在平面直角坐标系中,如图,矩形ABCO的边OA在x轴上,OC在y轴上,OA=4,OC=3.点Q从点C出发沿CB方向以每秒2个单位的速度向点B运动,以CQ为一边向下作正方形CQDE,同时点P从原点O出发在x轴上以每秒1个单位的速度向右运动,点Q的运动时间为x(s),△PBD的面积为y,当点Q到点B时,P、Q两点同时停止运动.回答下列问题:(1)点B的坐标为(4,3);
(2)当x=1时,求直线PB的解析式,并判断此时点D是否在直线PB上,说明理由;
(3)求y与x之间的函数关系式.
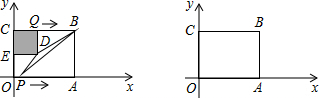
分析 (1)根据OA、OC的长度结合矩形的性质即可得出点B的坐标;
(2)当x=1时找出点P、Q的坐标,根据点P、B的坐标利用待定系数法即可求出直线PB的解析式,根据点Q的坐标结合正方形的性质即可得出点D的坐标,再根据一次函数图象上点的坐标特征验证此时点D是否在直线PB上;
(3)过点D作DF⊥x轴交直线PB于点F,设点P的坐标为(a,0),则点D的坐标为(2a,3-2a),根据点P、B的坐标利用待定系数法求出直线PB的解析式,再结合点D的坐标找出过点D、F的直线的解析式,由此即可得出点F的坐标,根据三角形的面积公式找出y关于a的关系式,将a换成x即可得出结论.
解答 解:(1)∵OA=4,OC=3,四边形ABCO为矩形,
∴AB=3,CB=4,
∴点B的坐标为(4,3).
故答案为(4,3).
(2)当x=1时,点P的坐标为(1,0),
设直线PB的解析式为y=kx+b,
∴$\left\{\begin{array}{l}{0=k+b}\\{3=4k+b}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=1}\\{b=-1}\end{array}\right.$,
∴直线PB的解析式为y=x-1.
∵点Q从点C出发沿CB方向以每秒2个单位的速度向点B运动,且x=1,
∴点Q(2,3),
∵四边形CQDE为正方形,
∴点D(2,1).
当x=2时,y=2-1=1,
∴此时点D在直线PB上.
(3)过点D作DF⊥x轴交直线PB于点F,如图所示.
设点P的坐标为(a,0),则点D的坐标为(2a,3-2a),
∵点B的坐标为(4,3),
利用待定系数法即可求出直线PB的解析式为y=$\frac{3}{4-a}$x+$\frac{3a}{a-4}$(0≤a≤2),
∵DF⊥x轴,
∴经过点D、F点的直线的解析式为x=2a,
∴点F的坐标为(2a,$\frac{3a}{4-a}$),
∴DF=|3-2a-$\frac{3a}{4-a}$|=$\frac{|2{a}^{2}-14a+12|}{4-a}$,
∴y=$\frac{1}{2}$DF•(xB-xP)=$\frac{1}{2}$×$\frac{|2{a}^{2}-14a+12|}{4-a}$×(4-a)=|a2-7a+6|.
将a换成x,
即可得出y=$\left\{\begin{array}{l}{{x}^{2}-7x+6(0≤x≤1)}\\{-{x}^{2}+7x-6(1<x≤2)}\end{array}\right.$.
点评 本题考查了矩形的性质、利用待定系数法求函数解析式、一次函数图象上点的坐标特征以及三角形的面积,解题的关键是:(1)根据矩形的性质找出点B的坐标;(2)利用待定系数法求出直线PB的解析式;(3)根据三角形的面积公式找出y关于x的函数关系式.本题属于中档题,难度不大,解决该题型题目时,根据点的坐标利用待定系数法求出函数解析式是关键.

 阅读快车系列答案
阅读快车系列答案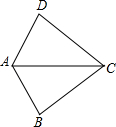 如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
如图,已知∠DAC=∠BAC,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )| A. | AB=AD | B. | ∠BCA=∠DCA | C. | CB=CD | D. | ∠ADC=∠ABC |
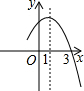 如图为二次函数y=ax2+bx+c的图象,在下列说法中:
如图为二次函数y=ax2+bx+c的图象,在下列说法中:①ac<0; ②方程ax2+bx+c=0的根是x1=-1,x2=3
③a+b+c>0 ④当x>1时,y随x的增大而增大.
正确的说法有①②③.
| A. | x2-1=x | B. | $\frac{1}{x}$+2=x | C. | 3x+$\frac{1}{2}$=$\frac{5-x}{3}$ | D. | 2x-y=1 |
| A. | 5ab-4ab=4 | B. | $\frac{1}{a}$+$\frac{1}{b}$=$\frac{2}{a+b}$ | C. | a6÷a2=a4 | D. | (a2b)3=a5b3 |
 如图所示的几何体的左视图是( )
如图所示的几何体的左视图是( )| A. |  | B. |  | C. |  | D. |  |
| A. | $\frac{2500}{x}$-$\frac{2500}{1.5x}$=5 | B. | $\frac{2500}{1.5x}$-$\frac{2500}{x}$=5 | ||
| C. | $\frac{1500}{1.5x}$=$\frac{1500}{x}$+5 | D. | $\frac{1000}{x}$+$\frac{1500}{1.5x}$=$\frac{2500}{x}$-5 |