题目内容
13．观察下列等式：
在上述数字宝塔中，从上往下数，2017在第44层．
分析 先按图示规律计算出每一层的第一个数和最后一个数；发现第一个数分别是每一层层数的平方，那么只要知道2017介于哪两个数的平方即可，通过计算可知：442＜2017＜452，则2017在第44层．
解答 解：第一层：第一个数为12=1，最后一个数为22-1=3，
第二层：第一个数为22=4，最后一个数为32-1=8，
第三层：第一个数为32=9，最后一个数为42-1=15，
∵442=1936，452=2025，
又∵1936＜2017＜2025，
∴在上述数字宝塔中，从上往下数，2017在第44层，
故答案为：44．
点评 本题考查了数学变化类的规律题，这类题的解题思路是：①从第一个数起，认真观察、仔细思考，能不能用平方或奇偶或加、减、乘、除等规律来表示；②利用方程来解决问题，先设一个未知数，找到符合条件的方程即可；本题以每一行的第一个数为突破口，找出其规律，得出结论．
练习册系列答案
新课标阶梯阅读训练系列答案
口算心算速算应用题系列答案
相关题目
4．明星队参加“希望杯”篮球比赛，在前8场比赛中的部分积分情况如表：
（1）求本次比赛中，胜一场和负一场各积多少分？
（2）前8场比赛结束时，某队是否存在胜场总积分等于它的负场总积分的情况？为什么？
（3）8场比赛以后还剩余m场比赛，当比赛结束时，该队是否存在胜场总积分等于它的负场总积分的情况？如果存在，求出胜场场次；如果不存在，请说明理由．
| 比赛场次 | 胜场 | 负场 | 积分 |
| m | 0 | m | m |
| 8 | 3 | 5 | 11 |
（2）前8场比赛结束时，某队是否存在胜场总积分等于它的负场总积分的情况？为什么？
（3）8场比赛以后还剩余m场比赛，当比赛结束时，该队是否存在胜场总积分等于它的负场总积分的情况？如果存在，求出胜场场次；如果不存在，请说明理由．
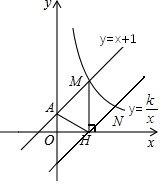如图，直线y=x+1与y轴交于点A，与反比例函数y=$\frac{k}{x}$（x＞0）的图象交于点M，MH⊥x轴于点H，tan∠AHO=$\frac{3}{2}$．
某景区修建一栋复古建筑，其窗户设计如图所示．圆O的圆心与矩形ABCD对角线的交点重合，且圆与矩形上下两边相切（E为上切点），与左右两边相交（F，G为其中两个交点），图中阴影部分为不透光区域，其余部分为透光区域．已知圆的半径为1m，根据设计要求，若∠EOF=45°，则此窗户的透光率（透光区域与矩形窗面的面积的比值）为$\frac{（π+2）\sqrt{2}}{8}$．