题目内容
8.某市决定购买A、B两种树苗对某段道路进行绿化改造,已知购买A种树苗9棵,B种树苗4棵,需要700元;购买A种树苗3棵,B种树苗5棵,则需要380元.(1)求购买A、B两种树苗每颗各需多少元?
(2)考虑到绿化效果和资金周转,购进A种树苗不能少于60棵,且用于购买这两种树苗的资金不能超过5260元.若购进这两种树苗共100棵,则有哪几种购买方案?哪种方案最省钱?
分析 (1)根据题意可以列出相应的方程组,从而可以求得购买A、B两种树苗每棵各需多少元;
(2)根据题意可以列出相应的不等式组,从而可以求得有几种购买方案和哪种方案最省钱.
解答 解:(1)设购买A种树苗每棵x元,B种树苗每棵y元,
$\left\{\begin{array}{l}{9x+4y=700}\\{3x+5y=380}\end{array}\right.$,得$\left\{\begin{array}{l}{x=60}\\{y=40}\end{array}\right.$,
答:购买A种树苗每棵60元,B种树苗每棵40元;
(2)设购买A种树苗a棵,
$\left\{\begin{array}{l}{60a+40(100-a)≤5260}\\{a≥60}\end{array}\right.$,
解得,60≤a≤63,
∴有四种购买方案,
方案一:购买A种树苗60棵,B种树苗40棵,
方案二:购买A种树苗61棵,B种树苗39棵,
方案三:购买A种树苗62棵,B种树苗38棵,
方案四:购买A种树苗63棵,B种树苗37棵,
∵A种树苗比B种树苗贵,
∴方案一最省钱.
点评 本题考查一元一次不等式组的应用、二元一次方程组的应用,解答此类问题的关键是明确题意,列出相应的方程组和不等式组,利用方程的思想和不等式的思想解答.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
11.某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
| A. | 平均数不变,方差不变 | B. | 平均数不变,方差变大 | ||
| C. | 平均数不变,方差变小 | D. | 平均数变小,方差不变 |
17.某学习小组9名学生参加“生活中的数学知识竞赛”,他们的得分情况如表:
那么这9名学生所得分数的众数和中位数分别是( )
| 人数(人) | 1 | 3 | 4 | 1 |
| 分数(分) | 80 | 85 | 90 | 95 |
| A. | 90,90 | B. | 90,85 | C. | 90,87.5 | D. | 85,85 |
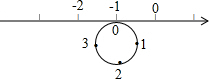 如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字3的点与数轴上表示-2的点重合…),则数轴上表示-10的点与圆周上表示数字3的点重合,数轴上表示-2016的点与圆周上表示数字1的点重合.
如图,圆的周长为4个单位长,数轴每个数字之间的距离为1个单位,在圆的4等分点处分别标上0、1、2、3,先让圆周上表示数字0的点与数轴上表示-1的点重合,再将数轴按逆时针方向环绕在该圆上(如圆周上表示数字3的点与数轴上表示-2的点重合…),则数轴上表示-10的点与圆周上表示数字3的点重合,数轴上表示-2016的点与圆周上表示数字1的点重合.