题目内容
16.小明沿着坡度i为1:$\sqrt{3}$的直路向上走了50m,则小明沿垂直方向升高了25m.分析 首先根据题意画出图形,由坡度为1:$\sqrt{3}$,可求得坡角∠A=30°,又由小明沿着坡度为1:$\sqrt{3}$的山坡向上走了50m,根据直角三角形中,30°所对的直角边是斜边的一半,即可求得答案.
解答 解:如图,过点B作BE⊥AC于点E,
∵坡度:i=1:$\sqrt{3}$,
∴tan∠A=1:$\sqrt{3}$=$\frac{\sqrt{3}}{3}$,
∴∠A=30°,
∵AB=50m,
∴BE=$\frac{1}{2}$AB=25(m).
∴他升高了25m.
故答案为:25.
点评 此题考查了坡度坡角问题.此题比较简单,注意能构造直角三角形并用解直角三角形的知识求解是解此题的关键,注意数形结合思想的应用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
11.某科普小组有5名成员,身高分别为(单位:cm):160,165,170,163,167.增加1名身高为165cm的成员后,现科普小组成员的身高与原来相比,下列说法正确的是( )
| A. | 平均数不变,方差不变 | B. | 平均数不变,方差变大 | ||
| C. | 平均数不变,方差变小 | D. | 平均数变小,方差不变 |
8.若一个三角形的两边长分别为2和4,则该三角形的周长可能是( )
| A. | 6 | B. | 7 | C. | 11 | D. | 12 |
5. 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
 如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )
如图,在△ABC中,点D,E分别在边AB,AC上,DE∥BC,若BD=2AD,则( )| A. | $\frac{AD}{AB}=\frac{1}{2}$ | B. | $\frac{AE}{EC}=\frac{1}{2}$ | C. | $\frac{AD}{EC}=\frac{1}{2}$ | D. | $\frac{DE}{BC}=\frac{1}{2}$ |
 如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B=70°.
如图,四边形ABCD中,AD∥BC,∠A=110°,则∠B=70°.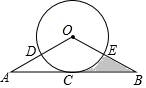 如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,$\widehat{CD}$=$\widehat{CE}$
如图,AB与⊙O相切于点C,OA,OB分别交⊙O于点D,E,$\widehat{CD}$=$\widehat{CE}$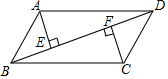 已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.
已知:如图,在平行四边形ABCD中,AE⊥BD,CF⊥BD,垂足分别为E,F.求证:△ADE≌△CBF.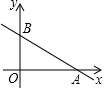 平面直角坐标系xOy中,点P的坐标为(m+1,m-1).
平面直角坐标系xOy中,点P的坐标为(m+1,m-1).