题目内容
18.已知$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$,且a,b,c都是正数,则$\frac{a+3b-2c}{2a+b}$=$\frac{3}{7}$.分析 设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$=k,从而可得到a=2k,b=3k,c=4k,然后求得代数式的值即可.
解答 解:设$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$=k,则a=2k,b=3k,c=4k.
故原式=$\frac{2k+9k-8k}{4k+3k}$=$\frac{3}{7}$.
故答案为:$\frac{3}{7}$.
点评 本题主要考查的是比例的性质,用含k的式子表示出a、b、c的值是解题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
8.读图填表


| 正方形个数 | 1 | 2 | 3 | 4 | … | n |
| 等腰三角形个数 | 0 | 4 | 8 | 12 | 4n-4 |
10.二次函数y=ax2+bx+c的部分对应值如下表:
二次函数y=ax2+bx+c图象的对称轴为x=2,x=-1对应的函数值y=-22.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | -54 | -36 | -12 | -6 | -6 | -22 | … |
8.若3a与2a+5互为相反数,则a等于( )
| A. | 5 | B. | -1 | C. | 1 | D. | -5 |
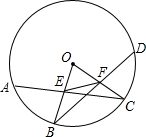 已知,如图,在⊙O中,$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,OB,OC分别交AC,BD于E,F,求证:OE=OF.
已知,如图,在⊙O中,$\widehat{AB}$=$\widehat{BC}$=$\widehat{CD}$,OB,OC分别交AC,BD于E,F,求证:OE=OF. 如图所示,∠ACB=90°,CD⊥AB,∠1与∠A,∠2与∠B有什么关系?用一个命题表达你所得到的结论为等角的余角相等.
如图所示,∠ACB=90°,CD⊥AB,∠1与∠A,∠2与∠B有什么关系?用一个命题表达你所得到的结论为等角的余角相等.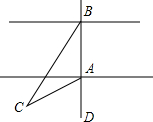 一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°,量出AC的长,它就是河宽(即A,B之间的距离),这个方法正确吗?请说明理由.
一次数学实践活动的内容是测量河宽,如图,即测量A,B之间的距离.同学们想出了许多方法,其中小聪的方法是:从点A出发,沿着与直线AB成60°角的AC方向前进至C,在C处测得∠C=30°,量出AC的长,它就是河宽(即A,B之间的距离),这个方法正确吗?请说明理由.