题目内容
3．
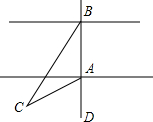一次数学实践活动的内容是测量河宽，如图，即测量A，B之间的距离．同学们想出了许多方法，其中小聪的方法是：从点A出发，沿着与直线AB成60°角的AC方向前进至C，在C处测得∠C=30°，量出AC的长，它就是河宽（即A，B之间的距离），这个方法正确吗？请说明理由．
分析 根据三角形外角的性质求得∠ABC=30°，证得∠ABC=∠C，根据等角对等边即可证得AB=AC．
解答 解：正确，
理由：∵∠CAD=60°，∠C=30°，
∴∠ABC=30°，
∴∠ABC=∠C，
∴AB=AC．
点评 本题考查了等腰三角形的判定和三角形外角的性质，熟练掌握性质定理是解题的关键．
练习册系列答案
相关题目
某生活小区的居民筹集资金1600元，计划在一块上，下两底分别为10m，20m的梯形空地种植花木．
15．
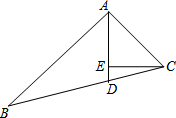如图，在△ABC中，AD平分∠BAC，CE⊥AD，垂足为E，∠ACE，∠B，∠ECD之间的数量关系是（ ）
如图，在△ABC中，AD平分∠BAC，CE⊥AD，垂足为E，∠ACE，∠B，∠ECD之间的数量关系是（ ）| A． | 2∠ACE=∠B+∠ECD | B． | ∠ACE=∠B+∠ECD | C． | ∠ACE=∠B+2∠ECD | D． | ∠ACE=2（∠B+∠ECD） |
12．下列说法正确的是（ ）
| A． | 等弧所对的弦相等 | |
| B． | 平分弦的直径垂直弦并平分弦所对的弧 | |
| C． | 若抛物线与坐标轴只有一个交点，则b2-4ac=0 | |
| D． | 相等的圆心角所对的弧相等 |