题目内容
6.已知12+22+32+42+…+n2=$\frac{1}{6}$(2n+1)(n+1)n.①求12+22+32+42+…+502的值.
②求262+272+282+292+…+502的值
③求22+42+62+82+…+502的值.
分析 ①根据12+22+32+42+…+n2=$\frac{1}{6}$(2n+1)(n+1)n,代入计算即可求解;
②262+272+282+292+…+502=(12+22+32+42+…+502)-(12+22+32+42+…+252),依此代入公式即可求解;
③22+42+62+82+…+502=22(12+22+32+42+…+252),依此代入公式即可求解.
解答 解:①12+22+32+42+…+502
=$\frac{1}{6}$×(2×50+1)×(50+1)×50
=42925.
②262+272+282+292+…+502
=(12+22+32+42+…+502)-(12+22+32+42+…+252)
=42925-$\frac{1}{6}$×(2×25+1)×(25+1)×25
=42925-5525
=37400.
③22+42+62+82+…+502
=22(12+22+32+42+…+252)
=4×5525
=22100.
点评 考查了有理数的混合运算,关键是熟练掌握12+22+32+42+…+n2=$\frac{1}{6}$(2n+1)(n+1)n的规律.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
15.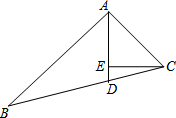 如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
 如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )
如图,在△ABC中,AD平分∠BAC,CE⊥AD,垂足为E,∠ACE,∠B,∠ECD之间的数量关系是( )| A. | 2∠ACE=∠B+∠ECD | B. | ∠ACE=∠B+∠ECD | C. | ∠ACE=∠B+2∠ECD | D. | ∠ACE=2(∠B+∠ECD) |
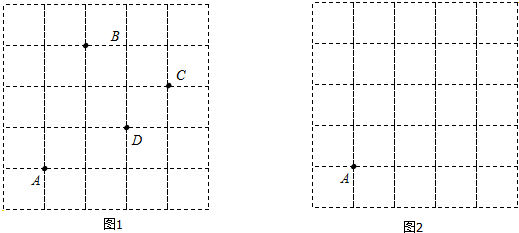
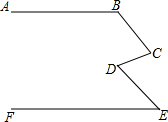 如图,直线AB∥EF,∠CDE=130°,求∠ABC+∠BCD+∠FED的度数.
如图,直线AB∥EF,∠CDE=130°,求∠ABC+∠BCD+∠FED的度数. 某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.
某生活小区的居民筹集资金1600元,计划在一块上,下两底分别为10m,20m的梯形空地种植花木.