题目内容
 如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.考点:全等三角形的判定与性质
专题:
分析:求出∠DAB=∠CAE,根据SAS推出△DAB≌△EAC,根据全等三角形的性质得出即可.
解答:证明:∵∠1=∠2,
∴∠1+∠EAB=∠2+∠EAB,
∴∠DAB=∠CAE,
在△DAB和△EAC中
∴△DAB≌△EAC,
∴∠B=∠C.
∴∠1+∠EAB=∠2+∠EAB,
∴∠DAB=∠CAE,
在△DAB和△EAC中
|
∴△DAB≌△EAC,
∴∠B=∠C.
点评:本题考查了全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,HL,全等三角形的对应边相等,对应角相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
在线段AB上选取3种点,第1种是将AB线段10等分的点;第2种是将AB线段12等分的点;第3种是将AB线段15等分的点,这些点连同AB线段的端点可组成线段的条数是( )
| A、350 | B、595 |
| C、666 | D、406 |
 正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),求D点的坐标(请写出解题过程).
正方形ABCD在平面直角坐标系中的位置如图所示,已知A点的坐标(0,4),B点的坐标(-3,0),求D点的坐标(请写出解题过程).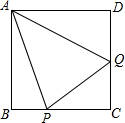 如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.
如图,正方形ABCD的边长为1,BC、CD上各有一点P、Q,若∠PAQ=45°,求△CPQ的周长.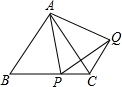 如图,△ABC为等边三角形,P点在BC上,△APQ为等边三角形.求证:AB∥CQ.
如图,△ABC为等边三角形,P点在BC上,△APQ为等边三角形.求证:AB∥CQ.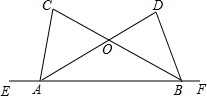 如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证:
如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.求证: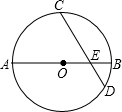 如图,⊙O的直径AB=8,点C为弧AB的中点,E为OB上一点,∠AEC=60°,CE的延长线交⊙O于D,求弦CD的长.
如图,⊙O的直径AB=8,点C为弧AB的中点,E为OB上一点,∠AEC=60°,CE的延长线交⊙O于D,求弦CD的长.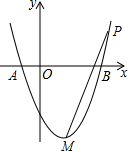 如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.
如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.