题目内容
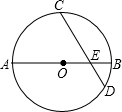如图，⊙O的直径AB=8，点C为弧AB的中点，E为OB上一点，∠AEC=60°，CE的延长线交⊙O于D，求弦CD的长．考点：垂径定理,勾股定理
专题：
分析：首先根据圆周角定理得出∠AOC=90°，再利用直角三角形中30°所对的边等于斜边的一半得出FO的长，再利用勾股定理得出答案．
解答：
解：如图所示：连接CO，过点O作OF⊥CD于点F，
∵⊙O的直径AB=8，点C为弧AB的中点，
∴CO⊥AB，
∵∠AEC=60°，
∴∠OCE=30°，
则FO=
CO=2，
CF=
=2
，
故弦CD的长为：4
．
解：如图所示：连接CO，过点O作OF⊥CD于点F，∵⊙O的直径AB=8，点C为弧AB的中点，
∴CO⊥AB，
∵∠AEC=60°，
∴∠OCE=30°，
则FO=
| 1 |
| 2 |
CF=
| 42-22 |
| 3 |
故弦CD的长为：4
| 3 |
点评：此题主要考查了垂径定理以及勾股定理和圆周角定理等知识，得出FO的长是解题关键．
练习册系列答案
相关题目
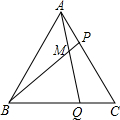如图，等边三角形ABC中，P、Q两点分别在AC、BC上，AP=CQ，AQ与BP交于点M，求证：∠BMQ=60°．
如图，已在AB=AC，AD=AE，∠1=∠2，求证：∠B=∠C．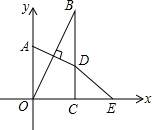
已知，如图在直角坐标系中，点A在y轴上，BC⊥x轴于点C，点A关于直线OB的对称点D恰好在BC上，点E与点O关于直线BC对称，∠OBC=35°，则∠OED=
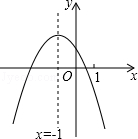二次函数y=ax2+bx+c （a≠0）的图象如图，给出下列四个结论：
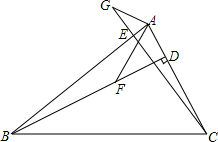已知：BD，CE是△ABC的高，点F在BD上，BF=AC，点G在CE的延长线上，CG=AB．