题目内容
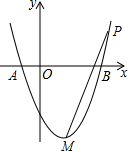 如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.
如图,抛物线y=x2-2x-3与x轴交于A,B两点,M为其顶点,P为拋物线第一象限内一点,若以PM为直径的⊙O′恰好过点A,求P点坐标.考点:圆的综合题
专题:
分析:由抛物线y=x2-2x-3与x轴交于A,B两点,可得A,B的坐标,由M为抛物线y=x2-2x-3的顶点,可得M的坐标.设P(x,y),可求得MP的中点N的坐标,可求得PM及AN的长,由PM=2AN,列出方程,化简得2y-x=1,由P(x,y)在抛物线y=x2-2x-3上,列出方程解得x的值,把x=
代入求出y的值,即可得出点P的坐标.
| 7 |
| 2 |
解答:解:∵抛物线y=x2-2x-3与x轴交于A,B两点,
∴令x2-2x-3=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∵M为抛物线y=x2-2x-3的顶点,
∴M(1,-4).设P(x,y),
∴MP的中点N的坐标为(
,
),
∴PM=
,
AN=
,
∵PM=2AN,
∴
=2
,化简得,2y-x=1,
又∵P(x,y)在抛物线y=x2-2x-3上,
∴
=x2-2x-3,解得x1=-1(舍去),x2=
,
把x=
代入y=
-7-3=
.
∴P(
,
).
∴令x2-2x-3=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0),
∵M为抛物线y=x2-2x-3的顶点,
∴M(1,-4).设P(x,y),
∴MP的中点N的坐标为(
| x+1 |
| 2 |
| y-4 |
| 2 |
∴PM=
| (x-1)2+(y+4)2 |
AN=
(
|
∵PM=2AN,
∴
| (x-1)2+(y+4)2 |
(
|
又∵P(x,y)在抛物线y=x2-2x-3上,
∴
| 1+x |
| 2 |
| 7 |
| 2 |
把x=
| 7 |
| 2 |
| 49 |
| 4 |
| 9 |
| 4 |
∴P(
| 7 |
| 2 |
| 9 |
| 4 |
点评:本题主要考查了圆的综合题,解题的关键是利用R=2r列出方程求解.

练习册系列答案
相关题目
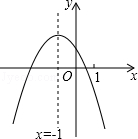 二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:
二次函数y=ax2+bx+c (a≠0)的图象如图,给出下列四个结论:①4ac-b2<0;②4a+c<2b;③3b+2c<0;④n(an+b)+b>a(n≠-1),
其中正确结论的个数是( )
| A、4个 | B、3个 | C、2个 | D、1个 |
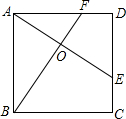 如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( )
如图,E、F分别是正方形的边CD、AD上的点,且CE=DF,AE、BF交于点O,下列结论正确的个数为( ) ①AE⊥BF;②AE=BF;③S△AOB=S四边形OEDF;④BO=OF.
| A、1个 | B、2个 | C、3个 | D、4个 |
12的算术平方根介于( )
| A、5和4之间 |
| B、4与3之间 |
| C、3与2之间 |
| D、2与1之间 |
 如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
如图,已在AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.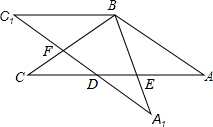 在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.
在△ABC中,AB=BC=4,∠ABC=120°,将△ABC绕点B旋转角α(0°<α<90°)得△A1BC1,A1B交AC于点E,A1C1分别交AC、BC于D、F两点.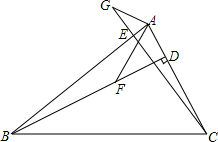 已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.
已知:BD,CE是△ABC的高,点F在BD上,BF=AC,点G在CE的延长线上,CG=AB.