题目内容
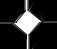
8. 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).(1)如果地面图案中正方形的面积是2,那么正八边形的面积是(4+4$\sqrt{2}$)cm2;
(2)如果地面图案中的正八边形边长为40,求地砖的边长.
(3)请你画出3种地砖的图案.
分析 (1)已知正方形的面积即可求得边长,然后根据正八边形与正方形的关系求解;
(2)根据(1)中的图形,正八边形可分成等腰直角三角形,根据等腰直角三角形的边角关系求解;
(3)根据图形把已知的图形分成全等的正方形即可.
解答 解:(1)正方形图案的边长即正八边形的边长是$\sqrt{2}$,
则正方形 的边长是$\sqrt{2}$+2×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2+$\sqrt{2}$,
的边长是$\sqrt{2}$+2×$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=2+$\sqrt{2}$,
则正八边形图案的面积是(2+$\sqrt{2}$)2-4×$\frac{1}{2}$×($\sqrt{2}$×$\frac{\sqrt{2}}{2}$)2=4+4$\sqrt{2}$.
故答案是:(4+4$\sqrt{2}$)cm2.
(2)地砖的边长是:40+2×40×$\frac{\sqrt{2}}{2}$=40+40$\sqrt{2}$(cm);
(3)把已知的图案分成全等的正方形即可. ,
, ,
, .
.
点评 本题考查了正多边形的计算,正确理解 中正八边形和正方形的边长之间的关系是关键.
中正八边形和正方形的边长之间的关系是关键.

练习册系列答案
相关题目
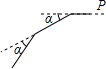 寒假里,小燕偶然发现爸爸手机有陀罗仪可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了108米.
寒假里,小燕偶然发现爸爸手机有陀罗仪可用来测量方位,于是她来到小区一处广场上.如图,小燕从P点向西直走12米后,向左转,转动的角度为α=40度,再走12米,再左转40度,如此重复,最终小燕又回到点P,则小燕一共走了108米.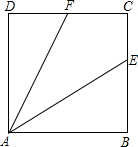 如图,正方形ABCD中,E为BC上一点.
如图,正方形ABCD中,E为BC上一点.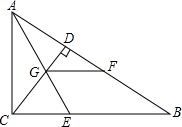 如图,∠ACB=90°,CD是高,角平分线AE交CD于G,点F在AB边上,AF=AC.猜想:GF与CB位置关系为GF∥CB,试证明你的猜想.
如图,∠ACB=90°,CD是高,角平分线AE交CD于G,点F在AB边上,AF=AC.猜想:GF与CB位置关系为GF∥CB,试证明你的猜想. 如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明: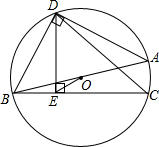 如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.
如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.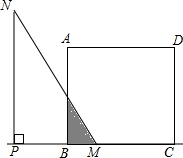 如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.
如图,正方形ABCD的边长为2cm,△PMN是直角一块三角板(∠N=30°),PM>2cm,PM与BC均在直线l上,开始时M点与B点重合,将三角板向右平行移动,直至M点与C点重合为止.设BM=xcm,三角板与正方形重叠部分的面积外ycm2.