题目内容
3.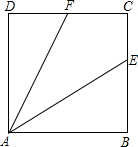 如图,正方形ABCD中,E为BC上一点.
如图,正方形ABCD中,E为BC上一点.(1)若AF平分∠DAE,求证:BE+DF=AE;
(2)若DF=CF,DC+CE=AE,求证:AF平分∠DAE.
分析 (1)如图1,延长CB到G,使BG=DF,连接AG,易证△ADF≌△ABG,得∠5=∠G,∠1=∠3,进而证明∠FAB=∠EAG,进而证明AE=EB+BG=EB+DF
(2)如图2,延长AF交BC的延长线于点G,由正方形的性质就可以得出△ADF≌△GCF,就有AD=CG,∠DAF=∠G,进而得出AE=GE,就有∠G=∠CAF,从而得出∠DAF=∠EAF而得出结论.
解答 证明:(1)延长CB到G,使BG=DF,连接AG(如图)
∵四边形ABCD是正方形,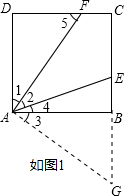
∴AD=AB,∠D=∠ABG=90°,
在△ADF和△ABG中,
$\left\{\begin{array}{l}{AD=AB}\\{∠D=∠ABG}\\{DF=BG}\end{array}\right.$,
∴△ADF≌△ABG(SAS),
∴∠5=∠G,∠1=∠3,
∵∠1=∠2,
∴∠2=∠3,
∴∠2+∠4=∠3+∠4,
即∠FAB=∠EAG,
∵CD∥AB,
∴∠5=∠FAB=∠EAG,
∴∠EAG=∠G,
∴AE=EB+BG=EB+DF;
(2)延长AF交BC的延长线于点G,
∵四边形ABCD是正方形,
∴AD=AB=DC,AD∥BC,
∴∠D=∠DCG=90°,∠DAF=∠G.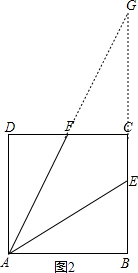
在△ADF和△GCF中,
$\left\{\begin{array}{l}{∠D=∠DCG}\\{∠DAF=∠G}\\{DF=CF}\end{array}\right.$,
∴△ADF≌△GCF(AAS),
∴AD=GC,
∴DC=GC.
∵DC+CE=AE,
∴GC+CE=AE,
∴GE=AE,
∴∠G=∠FAE,
∴∠DAF=∠EAF,
∴AF平分∠DAE.
点评 本题考查了正方形的性质的运用,全等三角形的判定及性质的运用,等腰三角形的性质的运用,角平分线的判定的运用,解答时证明三角形全等是关键.

| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
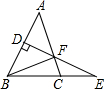 如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )| A. | 16cm,40° | B. | 8cm,50° | C. | 16cm,50° | D. | 8cm,40° |
| A. | a-3<b-3 | B. | a-b>0 | C. | $\frac{1}{3}a>\frac{1}{3}$b | D. | -2a<-2b |
 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).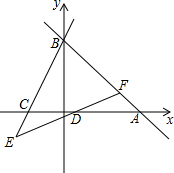 如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.
如图,直线y=-x+6与x轴交于点A,与y轴交于点B,C(-2,0),直线y=kx-k与x轴交于点D,交AB于F,交BC的延长线于E,若DE=DF,求k的值.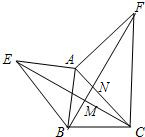 如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.
如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.