题目内容
13.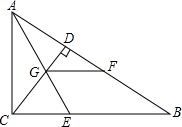 如图,∠ACB=90°,CD是高,角平分线AE交CD于G,点F在AB边上,AF=AC.猜想:GF与CB位置关系为GF∥CB,试证明你的猜想.
如图,∠ACB=90°,CD是高,角平分线AE交CD于G,点F在AB边上,AF=AC.猜想:GF与CB位置关系为GF∥CB,试证明你的猜想.
分析 连接CF,延长FG交AC于M,由AF=AC,AE平分∠CAF,根据三角形的三线合一性质得出AE⊥CF,AN是△ACF的高,由三角形的三条高交于一点得出MF是△ACF的高,证出MF∥CB即可.
解答 解:GF∥CB,理由如下:
连接CF,延长FG交AC于M,如图所示: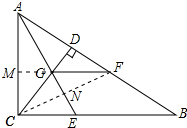 ∵AF=AC,AE平分∠CAF,
∵AF=AC,AE平分∠CAF,
∴AE⊥CF,
∴AN是△ACF的高,
∵CD是△ACF的高,三角形的三条高交于一点,
∴MF是△ACF的高,
∴MF⊥AC,
∴∠AMF=90°=∠ACB,
∴MF∥CB,
∴GF∥CB.
故答案为:GF∥CB.
点评 本题考查了等腰三角形的性质、平行线的判定、三角形三条高交于一点的性质;熟练掌握等腰三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
相关题目
3.小明每天坐爸爸的汽车上学都要经过三个只有红灯和绿灯的路口,假如每个路口红灯和绿灯亮的时间相同,那么小明从家随时出发去学校,他一次也没有遇到红灯的概率是多少?( )
| A. | $\frac{1}{16}$ | B. | $\frac{1}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{2}$ |
 在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积.
在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积. 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).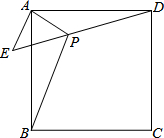 如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.
如图,已知ABCD为正方形,△AEP为等腰直角三角形,∠EAP=90°,EA=AP=1,且D、P、E三点共线,若PB=$\sqrt{5}$,则PC=$\sqrt{3}$.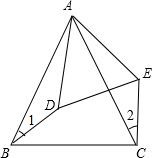 已知,∠BAC=∠DAE,∠1=∠2,且AB=AC,求证:BD=CE.
已知,∠BAC=∠DAE,∠1=∠2,且AB=AC,求证:BD=CE.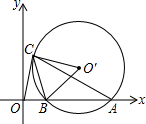 如图,⊙O′与x轴交于A,B两点,A($\sqrt{3}+1$,0),O′($\sqrt{3}$,1),过O点作⊙O′的切线,切点为C点,求BC的长.
如图,⊙O′与x轴交于A,B两点,A($\sqrt{3}+1$,0),O′($\sqrt{3}$,1),过O点作⊙O′的切线,切点为C点,求BC的长.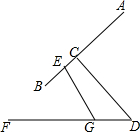 一台式电脑显示器的左视图如图所示,它由显示器侧边AB、支点四边形CEGD和底盘FD组成,若AB=28cm、EG=4$\sqrt{3}$cm,BE=3cm,∠EGF=60°,∠AEG=130°.若以FD所在直线为水平方向,求显示屏侧边AB相对于水平线FD的倾斜角度(用锐角表示).
一台式电脑显示器的左视图如图所示,它由显示器侧边AB、支点四边形CEGD和底盘FD组成,若AB=28cm、EG=4$\sqrt{3}$cm,BE=3cm,∠EGF=60°,∠AEG=130°.若以FD所在直线为水平方向,求显示屏侧边AB相对于水平线FD的倾斜角度(用锐角表示).