题目内容
19.Rt△ABC中,∠C=90°,AC=8cm,BC=6cm,以C为圆心5cm的长为半径作圆,则⊙C与AB所在直线的位置关系是( )| A. | 相离 | B. | 相切 | C. | 相交 | D. | 内含 |
分析 此题首先应求得圆心到直线的距离,根据直角三角形的面积公式即可求得;再进一步根据这些和圆的位置关系与数量之间的联系进行判断.
若d<r,则直线与圆相交;若d=r,则直线于圆相切;若d>r,则直线与圆相离.
解答 解:∵BC=6厘米,AC=8厘米,
∴AB=$\sqrt{{6}^{2}{+8}^{2}}$=10,S△ABC=$\frac{1}{2}$AC×BC=$\frac{1}{2}$×6×8=24,
∴AB上的高为:24×2÷10=4.8,
即圆心到直线的距离是4.8,
∵4.8<5,
∴直线和圆相交.
故选C.
点评 本题主要考查了直线与圆的位置关系,根据三角形的面积求出斜边上的高的长度是解答此题关键.
注意:直角三角形斜边上的高等于两条直角边的乘积除以斜边.

练习册系列答案
相关题目
14.已知⊙O1与⊙O2的半径分别为3cm和4cm,两元的圆心距为7cm,则两圆的位置关系为( )
| A. | 外离 | B. | 外切 | C. | 相交 | D. | 内含 |
11.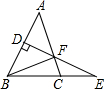 如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
 如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )
如图所示,在△ABC中,AB=AC,AB的垂直平分线DE交BC的延长线于E,交AC于F,连接BF,∠A=50°,AB+BC=16cm,则△BCF的周长和∠EFC分别等于( )| A. | 16cm,40° | B. | 8cm,50° | C. | 16cm,50° | D. | 8cm,40° |
9.一个多边形的内角和为1080°,则它的边数为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
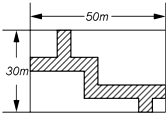 如图所示,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为2米,其他部分均种植花草,则种植花草的面积是1344米2.
如图所示,在长为50米,宽为30米的长方形地块上,有纵横交错的几条小路(图中阴影部分),宽均为2米,其他部分均种植花草,则种植花草的面积是1344米2.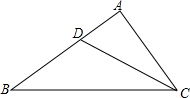 如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).
如图,△ABC中,已知∠A=2∠B,CD是∠ACB的平分线,试说明BC=AD+AC.(提示:在BC边上取点E,使EC=AC,联结DE).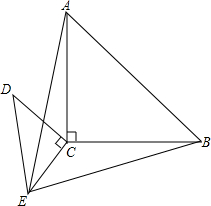 把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC
把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC 在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积.
在长为30,宽为20的矩形纸片上,如图所示剪去四个边长为x的小正方形,若剪去部分的面积等于剩余部分的面积. 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).