题目内容
17.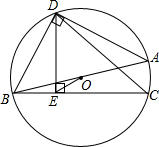 如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.
如图,AB为⊙O的直径,D为半圆的中点,DE⊥弦BC于E,连接BD,OE.(1)求证:OE⊥CD;
(2)若BE=2,OE=$\sqrt{2}$,求BD的长.
分析 (1)连接OD、OC,要证OE⊥CD,只要证DE=EC,OE平分∠DEC,由D为半圆的中点,DE⊥弦BC于E,易得△DOE≌△COE,进而得出结论;
(2)作OH⊥EC,运用等腰直角三角形的性质和勾股定理计算即可.
解答 解:(1)证明:连接OD、OC,
∵D为半圆的中点,
∴$\widehat{AD}=\widehat{BD}$
∴∠A=∠BCD=45°
∵DE⊥BC
∴∠CED=90°
∴∠CDE=∠DCE
∴CE=DE
在△DOE和△COE中,
$\left\{\begin{array}{l}{DE=CE}\\{OD=OC}\\{OE=OE}\end{array}\right.$,
∴△DOE≌△COE,
∴∠DEO=∠CEO
∴OE⊥CD;
(2)作OH⊥EC,
∵∠OEH=45°,OE=$\sqrt{2}$,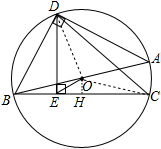
∴OH=EH=1
∵BE=2,
∴BH=3
∴BO=$\sqrt{10}$
∵∠ABD=45°OD⊥AB
∴△BOD是等腰直角三角形
∴BD=$\sqrt{2}$OB=2$\sqrt{5}$.
点评 本题考查了圆周角定理,三角形全等的判定和性质,等腰直角三角形的判定和性质以及勾股定理的运用,有一定的综合性,难度适中.

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
9.一个多边形的内角和为1080°,则它的边数为( )
| A. | 9 | B. | 8 | C. | 7 | D. | 6 |
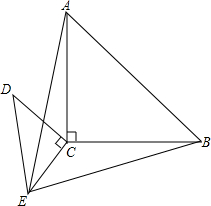 把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC
把两个含有45°角的等腰直角三角板直角顶点重合放在一起,如图所示,∠ACB=∠DCE=90°,DC=EC,AC=BC 用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).
用同样图案的正方形地砖,铺成如图所示的正方形和正八边形相间的地面图案(地砖与地砖拼接线忽略不计).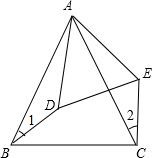 已知,∠BAC=∠DAE,∠1=∠2,且AB=AC,求证:BD=CE.
已知,∠BAC=∠DAE,∠1=∠2,且AB=AC,求证:BD=CE.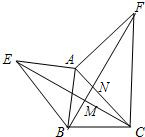 如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.
如图所示,已知AE=AB,AF=AC,EC=BF,求证:∠CMF=∠CAF.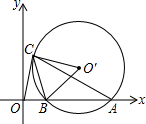 如图,⊙O′与x轴交于A,B两点,A($\sqrt{3}+1$,0),O′($\sqrt{3}$,1),过O点作⊙O′的切线,切点为C点,求BC的长.
如图,⊙O′与x轴交于A,B两点,A($\sqrt{3}+1$,0),O′($\sqrt{3}$,1),过O点作⊙O′的切线,切点为C点,求BC的长.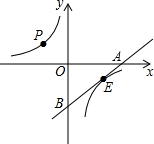 如图,点P(-2,3)在双曲线上,点E为该双曲线在第四象限图象上一动点,过E的直线与双曲线只有一个公共点,并与x轴和y轴分别交于A、B两点,则△AOB面积为( )
如图,点P(-2,3)在双曲线上,点E为该双曲线在第四象限图象上一动点,过E的直线与双曲线只有一个公共点,并与x轴和y轴分别交于A、B两点,则△AOB面积为( )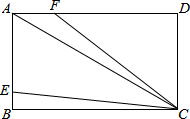 如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.
如图,AC是矩形ABCD的对角线,AB=2,BC=2$\sqrt{3}$,点E,F分别是线段AB,AD上的点,连接CE,CF.当∠BCE=∠ACF,且CE=CF时,AE+AF=$\frac{4\sqrt{3}}{3}$.