题目内容
4. 如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少?
如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少?
分析 当AD=8时,取AB的中点M,连接MF和CM,可知CF的最大值为4+3$\sqrt{5}$.即可得到线段CF长度的最大值.
解答  解:如图,取AB的中点M,连接MF和CM,
解:如图,取AB的中点M,连接MF和CM,
∵将线段AD绕点A旋转至AD′,
∴AD′=AD=8,
∵∠ACB=90°,
∵AC=12,BC=6,
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}$=6$\sqrt{5}$.
∵M为AB中点
∴CM=3$\sqrt{5}$,
∵AD′=8.
∵M为AB中点,F为BD′中点,
∴FM=$\frac{1}{2}$AD′=4.
如图:∴当且仅当M、F、C三点共线且M在线段CF上时CF最大,
此时CF=CM+FM=4+3$\sqrt{5}$.
点评 本题考查了三角形相似的判定与性质.旋转的性质和三角函数的定义以及直角三角形斜边上的中线等于斜边的一半,知道当且仅当M、F、C三点共线且M在线段CF上时CF最大是解题的关键.

练习册系列答案
相关题目
14.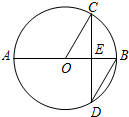 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )| A. | $\frac{3}{2}$cm | B. | $\frac{3}{2}$$\sqrt{3}$cm | C. | 3$\sqrt{3}$cm | D. | 6cm |
15.下列命题中正确的是( )
| A. | 对角线相等的四边形是矩形 | |
| B. | 对角相等有一个角是直角的四边形是矩形 | |
| C. | 有一个角是直角的四边形是矩形 | |
| D. | 内角都相等的四边形是矩形 |
 如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如;当x=1时,y1=0,y2=4,y1<y2,此时M=0,下列判断中正确的是( )
如图,已知抛物线y1=-2x2+2,直线y2=2x+2,当x任取一值时,x对应的函数值分别为y1、y2.若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.例如;当x=1时,y1=0,y2=4,y1<y2,此时M=0,下列判断中正确的是( ) 如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.
如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把△ABE沿AE折叠,使点B落在点F处,当△CEF为直角三角形时,CF的长为4或2$\sqrt{10}$.
如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把△ABE沿AE折叠,使点B落在点F处,当△CEF为直角三角形时,CF的长为4或2$\sqrt{10}$. 甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD.如图所示.
甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD.如图所示. 如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2=$\frac{6}{x}$图象的一个交点.
如图,已知点A(a,3)是一次函数y1=x+b图象与反比例函数y2=$\frac{6}{x}$图象的一个交点.