题目内容
13. 甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD.如图所示.
甲、乙两台机器共同加工一批零件,在加工过程中两台机器均改变了一次工作效率.从工作开始到加工完这批零件两台机器恰好同时工作6小时.甲、乙两台机器各自加工的零件个数y(个)与加工时间x(时)之间的函数图象分别为折线OA-AB与折线OC-CD.如图所示.(1)求甲机器改变工作效率前每小时加工零件的个数.
(2)求乙机器改变工作效率后y与x之间的函数关系式.
(3)求这批零件的总个数.
分析 (1)甲改变工作效率前的工作效率为改变前加工的总件数,除以加工的总时间即可;
(2)利用待定系数法求一次函数解析式即可;
(3)利用函数解析式求出甲、乙两机器6小时加工的总件数,求其和即可.
解答 解:(1)80÷4=20(件);
(2)设AB与CD的交点为P,由图可以P坐标为(5,110)
∵图象过C(2,80),P(5,110),
∴设解析式为y=kx+b(k≠0),
∴$\left\{\begin{array}{l}{2k+b=80}\\{5k+b=110}\end{array}\right.$,解得:$\left\{\begin{array}{l}{k=10}\\{b=60}\end{array}\right.$,
∴y乙=10x+60(2≤x≤6);
(3)∵AB过(4,80),P(5,110),
∴设AB的解析式为y甲=mx+n(m≠0),
∴$\left\{\begin{array}{l}{4m+n=80}\\{5m+n=110}\end{array}\right.$,解得:$\left\{\begin{array}{l}{m=30}\\{n=-40}\end{array}\right.$,
∴y甲=30x-40(4≤x≤6),
当x=6时,y甲=30×6-40=140,y乙=10×6+60=120,
∴这批零件的总个数是140+120=260.
点评 此题主要考查了一次函数的应用,根据题意得出函数关系式以及数形结合是解决问题的关键.

练习册系列答案
相关题目
8.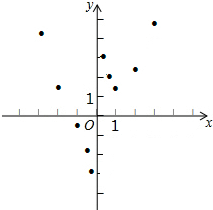 有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
小东根据学习函数的经验,对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
求m的值;
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值.
 有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.小东根据学习函数的经验,对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值.
5.正n边形每个内角的大小都为108°,则n=( )
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
 如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元.
如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元. 如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少?
如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少? 如图,矩形OABC,A(0,5),C(4,0),正比例函数y=mx(m≠0)的图象经过点B.
如图,矩形OABC,A(0,5),C(4,0),正比例函数y=mx(m≠0)的图象经过点B. 如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,CD与BD交于点D.
如图,已知BD是△ABC的角平分线,CD是△ABC的外角∠ACE的平分线,CD与BD交于点D. 如图,一次函数y=kx+b的图象与反比例函数y=-$\frac{7}{x}$的图象交于A(-1,m)、B(n,-1)两点
如图,一次函数y=kx+b的图象与反比例函数y=-$\frac{7}{x}$的图象交于A(-1,m)、B(n,-1)两点