题目内容
14.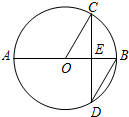 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )
如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,⊙O的半径为3cm,则CD弦长为( )| A. | $\frac{3}{2}$cm | B. | $\frac{3}{2}$$\sqrt{3}$cm | C. | 3$\sqrt{3}$cm | D. | 6cm |
分析 根据圆周角定理可求出∠COB的度数,再利用特殊角的三角函数值及垂径定理即可解答.
解答 解:∵∠CDB=30°,
∴∠COB=60°,
又∵OC=3cm,CD⊥AB于点E,
∴OE=$\frac{3}{2}$,
解得CE=$\frac{3}{2}$$\sqrt{3}$cm,
∴CD=3$\sqrt{3}$cm.
故选C.
点评 本题考查了垂径定理、勾股定理以及解直角三角形.此题难度不大,注意数形结合思想的应用.

练习册系列答案
相关题目
 已知:AD⊥AB,DE平分∠ADC,CE平分∠BCD,∠1+∠2=90°,求证:BC⊥AB.
已知:AD⊥AB,DE平分∠ADC,CE平分∠BCD,∠1+∠2=90°,求证:BC⊥AB.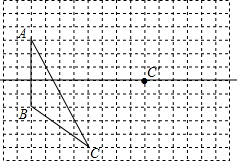 画图并填空:如图,方格纸中每个小正方形的边长都为1.
画图并填空:如图,方格纸中每个小正方形的边长都为1. 如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元.
如图,A、B两个小镇在河流的同侧,它们到河流的距离AC=10千米,BD=30千米,且CD=30千米,现要在河流边修建一自来水厂分别向两镇供水,铺设水管的费用为每千米3万元. 如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少?
如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少?