题目内容
19. 如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.
如图,在平面直角坐标系中,二次函数y=-x2+bx的图象经过点A(4,0).点E是过点C(2,0)且与y轴平行的直线上的一个动点,过线段CE的中点G作DF⊥CE交二次函数的图象于D、F两点.(1)求二次函数的表达式.
(2)当点E落在二次函数的图象的顶点上时,求DF的长.
(3)当四边形CDEF是正方形时,请直接写出点E的坐标.
分析 (1)把A点的坐标代入抛物线的解析式,求出b的值即可得到抛物线的解析式;
(2)由(1)可知抛物线的顶点坐标,因为G是EC中点,由此可求出G的纵坐标,代入抛物线的解析式可求出F和D的横坐标,进而可求出DF的长;
(3)四边形CDEF是正方形时可设E(2,2m),则F(2-m,m),把F点的坐标代入解析式即可求出m的值,进而可求出点E的坐标.
解答 解:(1)把(4,0)代入y=-x2+bx中,得b=4.
∴二次函数的表达式为y=-x2+4x.
(2)由(1)可知二次函数的图象的顶点坐标为(2,4),
∵G是EC的中点,
∴当y=2时,-x2+4x=2.
∴x1=2-$\sqrt{2}$,x2=2+$\sqrt{2}$,
∴DF=2+$\sqrt{2}$-(2-$\sqrt{2}$)=2$\sqrt{2}$.
(3)设E(2,2m),则F(2-m,m).
∵点F在抛物线上,
∴m=-(2-m)2+4(2-m).
∴m=$\frac{1±\sqrt{17}}{2}$,2m=-1±$\sqrt{17}$.
∴E1(2,-1+$\sqrt{17}$),E2=(2,-1-$\sqrt{17}$).
点评 本题考查了用待定系数法求二次函数的解析式、解一元二次方程以及正方形的性质,题目的综合性较强,难度中等.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
10.某天放学后,小敏徒步回家,如图所示,反映了她的速度与时间的变化关系.
(1)请你根据图象填写下表:
(2)根据图象或表格你能叙述一下小敏行走的情况吗?

(1)请你根据图象填写下表:
| 时间/分 | 0 | 2 | 4 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 24 |
| 速度/(千米/时) |

8. 有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
小东根据学习函数的经验,对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
求m的值;
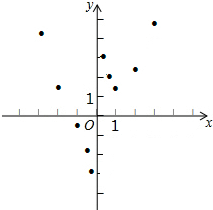
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值.
 有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.
有这样一个问题:探究函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质.小东根据学习函数的经验,对函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的图象与性质进行了探究.
下面是小东的探究过程,请补充完整:
(1)函数y=$\frac{1}{2}$x2+$\frac{1}{x}$的自变量x的取值范围是x≠0;
(2)下表是y与x的几组对应值.
| x | … | -3 | -2 | -1 | -$\frac{1}{2}$ | -$\frac{1}{3}$ | $\frac{1}{3}$ | $\frac{1}{2}$ | 1 | 2 | 3 | … |
| y | … | $\frac{25}{6}$ | $\frac{3}{2}$ | -$\frac{1}{2}$ | -$\frac{15}{8}$ | -$\frac{53}{18}$ | $\frac{55}{18}$ | $\frac{17}{8}$ | $\frac{3}{2}$ | $\frac{5}{2}$ | m | … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是(1,$\frac{3}{2}$),结合函数的图象,写出该函数的其它性质(一条即可)该函数没有最大值.
 如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$.其中正确的是①②④(写出所有正确结论的序号).
如图,AB是⊙O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足$\frac{CF}{FD}$=$\frac{1}{3}$,连接AF并延长交⊙O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=2;③tan∠E=$\frac{\sqrt{5}}{2}$;④S△DEF=4$\sqrt{5}$.其中正确的是①②④(写出所有正确结论的序号). 小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题:
小刚和小强相约晨练跑步,小刚比小强早1分钟离开家门,3分钟后迎面遇到从家跑来的小强.两人同路并行跑了2分钟后,决定进行长跑比赛,比赛时小刚的速度始终是180米/分,小强的速度始终是220米/分.下图是两人之间的距离y(米)与小刚离开家的时间x(分钟)之间的函数图象,根据图象回答下列问题: 如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少?
如图,已知△ABC中,∠ACB=90°,BC=6,AC=12,点D在AC上,且AD=8,将线段AD绕点A旋转至AD′,F为BD′的中点,线段CF的最大值为多少? 如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1=$\frac{k}{x}$图象经过点C,一次函数y2=ax+b的图象经过点A、C
如图,四边形ABCD为正方形.点A的坐标为(0,2),点B的坐标为(0,-3).反比例函数y1=$\frac{k}{x}$图象经过点C,一次函数y2=ax+b的图象经过点A、C