题目内容
13．
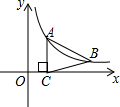如图，点A、B在双曲线y=$\frac{k}{x}$（x＞0）上，AC⊥x轴于C，且AB=BC，若S△ABC=6，求k的值．
分析 设A（a，$\frac{k}{a}$），根据已知条件和等腰三角形的性质得出B的纵坐标为$\frac{k}{2a}$，代入解析式求得横坐标，然后根据S△ABC=$\frac{1}{2}$•$\frac{k}{a}$•（2a-a）=6，即可求得k的值．
解答 解：设A（a，$\frac{k}{a}$），
∵AC⊥x轴于C，且AB=BC，
∴B的纵坐标为$\frac{k}{2a}$，
代入y=$\frac{k}{x}$得$\frac{k}{2a}$=$\frac{k}{x}$，
∴x=2a，
∴B（2a，$\frac{k}{2a}$），
∵S△ABC=6，
∴$\frac{1}{2}$•$\frac{k}{a}$•（2a-a）=6，
解得k=12．
点评 本题考查了反比例系数k的几何意义，等腰三角形的性质以及三角形面积等，由A的坐标根据等腰三角形的性质和反比例函数图象上点的坐标特征表示出B的坐标是解题的关键．
练习册系列答案
优学名师名题系列答案
相关题目
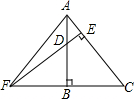已知：如图，FE、AB分别是△ACF的边AC、FC上的高，DB=BC．求证：AB=BF．
如图，△BEF的面积比△ADF的面积少24cm2，△ABD的面积与△CDE的面积比是4：5，求平行四边形ABCD的面积．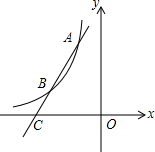
已知反比例函数y=$\frac{m-8}{x}$（m8≠8且m为常数）的图象经过点A（-1，6）．
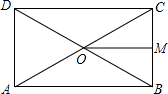已知：如图，在?ABCD中，对角线AC，BD交于点O，OM⊥BC于点M，且BM=CM，求证：?ABCD是矩形．
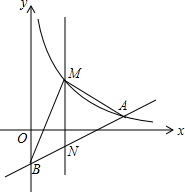如图，在平面直角坐标系中，已知点A（8，1），B（0，-3），反比例函数y=$\frac{k}{x}$（x＞0）的图象经过点A，N是线段AB上一动点（不与A、B重合），MN⊥x轴且与反比例函数的图象交于M点．
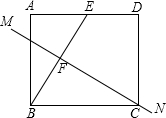如图，长方形纸片ABCD中，CD=4，点E是AD上的-点，且AE=2，BE的垂直平分线MN恰好过点C，求矩形的一边AD的长度．
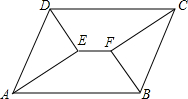如图，?ABCD中，AB＞AD，∠A与∠D的平分线交于点E，∠B与∠C的平分线交于点F，连接EF．请证明：EF=AB-BC．