题目内容
15. 以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.
以等腰△ABC的腰AB为直径作半圆,设圆心为点O,半圆与另一腰交于点D,与底BC交于点E,取线段CD的中点F,连接EF.(1)证明:EF切半圆于E;
(2)证明:阴影部分与△EFC的面积相等.
分析 (1)连接BD交OE于点G,分别证BD∥EF、OE∥AC可知四边形EFDG是矩形,由切线判定可得;
(2)由(1)知OE⊥BD,根据垂径定理可得DE=BE、$\widehat{DE}=\widehat{BE}$,从而可知阴影部分面积=S△DEF,再根据HL证△DEF≌△CEF即可得.
解答 证明:(1)连接BD,交OE于点G,
∵AB是⊙O的直径,
∴BD⊥AC,
又∵EF⊥AC,
∴∠EFC=90°,BD∥EF,
∵E是BC中点,O是AB中点,
∴EO∥AC,
∴四边形EFDG是矩形,
∴∠OEF=90°,
∵OE是⊙O的半径,
∴EF切半圆于E;
(2)连接DE,
由(1)知∠OEF=90°,BD∥EF,
∴∠OGE=90°,即OE⊥BD,
∴DE=BE,$\widehat{DE}=\widehat{BE}$,
∴弓形BE的面积=弓形DE的面积,
∴阴影部分面积=S△DEF,
又∵BE=CE,
∴DE=CE,
在RT△DEF和RT△CEF中,
$\left\{\begin{array}{l}{DE=CE}\\{EF=EF}\end{array}\right.$,
∴△DEF≌△CEF(HL),
∴S△CEF=S△DEF,
故阴影部分与△EFC的面积相等.
点评 本题主要考查切线的判定及垂径定理的应用,切线的判定常用的方法是利用切线的判定定理转化为证明垂直的问题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
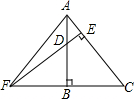 已知:如图,FE、AB分别是△ACF的边AC、FC上的高,DB=BC.求证:AB=BF.
已知:如图,FE、AB分别是△ACF的边AC、FC上的高,DB=BC.求证:AB=BF. 如图,△BEF的面积比△ADF的面积少24cm2,△ABD的面积与△CDE的面积比是4:5,求平行四边形ABCD的面积.
如图,△BEF的面积比△ADF的面积少24cm2,△ABD的面积与△CDE的面积比是4:5,求平行四边形ABCD的面积.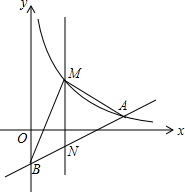 如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,N是线段AB上一动点(不与A、B重合),MN⊥x轴且与反比例函数的图象交于M点.
如图,在平面直角坐标系中,已知点A(8,1),B(0,-3),反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,N是线段AB上一动点(不与A、B重合),MN⊥x轴且与反比例函数的图象交于M点.