题目内容
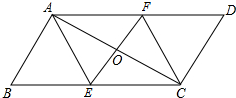 如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.
如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.(1)证明:△AOF≌△OCE;
(2)证明:四边形AECF是平行四边形;
(3)当△ABC满足什么条件时(只能添加一个条件),四边形AECF是矩形.
考点:平行四边形的判定与性质,全等三角形的判定与性质,矩形的判定
专题:
分析:(1)利用平行四边形的性质证明AF=CE,利用全等三角形的判定方法即可证得;
(2)根据一组对边平行且相等的四边形是平行四边形即可判断;
(3)根据矩形的判定定理或定义即可直接写出答案.
(2)根据一组对边平行且相等的四边形是平行四边形即可判断;
(3)根据矩形的判定定理或定义即可直接写出答案.
解答:解:(1)∵四边形ABCD是平行四边形,
∴AD=BC,
又∵E、F分别为BC、AD的中点,
∴AF=CE,
又∵平行四边形ABCD,AD∥BC,
∴∠FAO=∠ECO,
∴在△AOF和△OCE中,
,
∴△AOF≌△OCE;
(2)∵AD∥BC,AF=CE,
∴四边形AECF是平行四边形;
(3)添上条件:AE⊥BC.(答案不唯一).
∴AD=BC,
又∵E、F分别为BC、AD的中点,
∴AF=CE,
又∵平行四边形ABCD,AD∥BC,
∴∠FAO=∠ECO,
∴在△AOF和△OCE中,
|
∴△AOF≌△OCE;
(2)∵AD∥BC,AF=CE,
∴四边形AECF是平行四边形;
(3)添上条件:AE⊥BC.(答案不唯一).
点评:本题考查了平行四边形的性质和判定方法,正确理解平行四边形的性质以及判定定理是关键.

练习册系列答案
相关题目
抽样调查某班学生的身高为(以160cm为基准,超过得记为正,不足的记为负,单位cm):1、-4、2、
-2.5、-2、1、7、-6、-9,这组数据的众数和中位数分别是( )
-2.5、-2、1、7、-6、-9,这组数据的众数和中位数分别是( )
| A、161,158 |
| B、161,167 |
| C、167,158 |
| D、167,161 |
 如图所示,已知∠AOC=∠BOC=90°,∠BOE=∠COD,则图中互为余角的角共有( )
如图所示,已知∠AOC=∠BOC=90°,∠BOE=∠COD,则图中互为余角的角共有( )| A、2对 | B、3对 | C、4对 | D、5对 |
一份稿件,甲单独打字需a小时完成,乙单独打字需b小时完成,若两人合打这份稿件,需( )完成.
| A、(a+b)小时 | ||
B、
| ||
C、
| ||
D、
|
 如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E,交AC于点F.求证:2AD=PE+PF.
如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E,交AC于点F.求证:2AD=PE+PF.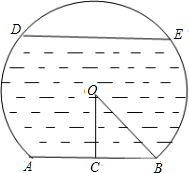 一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=