题目内容
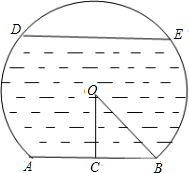 一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=
一个弓形桥洞截面示意图如图所示,圆心为O,弦AB是水底线,OC⊥AB,AB=24m,sin∠COB=| 12 |
| 13 |
(1)当水位线DE=4
| 30 |
(2)若水位线以一定的速度下降,当水深8m时,求此时∠ACD的余切值.
考点:垂径定理的应用,勾股定理
专题:
分析:(1)延长CO交DE于点F,连接OD,根据垂径定理求出BC的长,由sin∠COB=
得出OB的长,根据DE∥AB可知∠ACD=∠CDE,∠DFO=∠BCO=90°.由OF过圆心可得出DF的长,再根据勾股定理求出OF的长,进而可得出CF的长;
(2)若水位线以一定的速度下降,当水深8m时,即CF=8m,则OF=CF-OC=3m,连接CD,在Rt△ODF中由勾股定理求出DF的长,由cot∠ACD=cot∠CDF即可得出结论.
| BC |
| OB |
(2)若水位线以一定的速度下降,当水深8m时,即CF=8m,则OF=CF-OC=3m,连接CD,在Rt△ODF中由勾股定理求出DF的长,由cot∠ACD=cot∠CDF即可得出结论.
解答: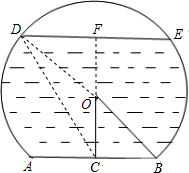 解:(1)延长CO交DE于点F,连接OD
解:(1)延长CO交DE于点F,连接OD
∵OC⊥AB,OC过圆心,AB=24m,
∴BC=
AB=12m.
在Rt△BCO中,sin∠COB=
=
,
∴OB=13mCO=5m.
∵DE∥AB,
∴∠ACD=∠CDE,∠DFO=∠BCO=90°.
又∵OF过圆心,
∴DF=
DE=
×4
=2
m.
在Rt△DFO中,OF=
=
=7m,
∴CF=CO+OF=12m,即当水位线DE=4
m时,此时的水深为12m;
(2)若水位线以一定的速度下降,当水深8m时,即CF=8m,则OF=CF-OC=3m,
连接CD,在Rt△ODF中,DF=
=
=4
m.
在Rt△CDF中,cot∠CDF=
=
.
∵DE∥AB,
∴∠ACD=∠CDE,
∴cot∠ACD=cot∠CDF=
.
答:若水位线以一定的速度下降,当水深8m时,此时∠ACD的余切值为
.
 解:(1)延长CO交DE于点F,连接OD
解:(1)延长CO交DE于点F,连接OD∵OC⊥AB,OC过圆心,AB=24m,
∴BC=
| 1 |
| 2 |
在Rt△BCO中,sin∠COB=
| BC |
| OB |
| 12 |
| 13 |
∴OB=13mCO=5m.
∵DE∥AB,
∴∠ACD=∠CDE,∠DFO=∠BCO=90°.
又∵OF过圆心,
∴DF=
| 1 |
| 2 |
| 1 |
| 2 |
| 30 |
| 30 |
在Rt△DFO中,OF=
| OD2-DF2 |
| 169-120 |
∴CF=CO+OF=12m,即当水位线DE=4
| 30 |
(2)若水位线以一定的速度下降,当水深8m时,即CF=8m,则OF=CF-OC=3m,
连接CD,在Rt△ODF中,DF=
| OD2-OF2 |
| 132-32 |
| 10 |
在Rt△CDF中,cot∠CDF=
| DF |
| CF |
| ||
| 2 |
∵DE∥AB,
∴∠ACD=∠CDE,
∴cot∠ACD=cot∠CDF=
| ||
| 2 |
答:若水位线以一定的速度下降,当水深8m时,此时∠ACD的余切值为
| ||
| 2 |
点评:本题考查的是垂径定理的应用,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
相关题目
买一个足球需要m元,买一个篮球需要n元,则买4个足球、7个篮球共需要( )
| A、(4m+7n)元 |
| B、28mn元 |
| C、(7m+4n)元 |
| D、11mn元 |
黄河农场各用10块面积相同的试验田种植甲、乙两种麦子,收获后对两种麦子产量(单位:吨/亩)的数据统计如下:
甲=0.61,
乙=0.59,S甲2=0.01,S乙2=0.002,则由上述数据推断乙种麦子产量比较稳定的依据是( )
. |
| x |
. |
| x |
A、
| ||||
| B、S甲2>S乙2 | ||||
C、
| ||||
D、
|
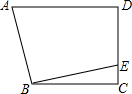 如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,BC=CD=8,过点B作EB⊥AB,交CD于点E.若DE=6,则AD的长为( )| A、6 | B、8 | C、10 | D、无法确定 |
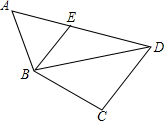 如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )
如图,在四边形ABCD中,∠A=58°,∠C=100°,连接BD,E是AD上一点,连接BE,∠EBD=36°.若点A,C分别在线段BE,BD的中垂线上,则∠ADC的度数为( )| A、75° | B、65° |
| C、63° | D、61° |
下列各式计算正确的是( )
| A、2a+2=3a2 |
| B、(-b3)2=-b6 |
| C、c2•c3=c5 |
| D、(m-n)2=m2-n2 |
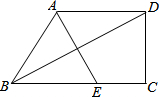 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是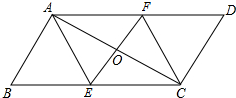 如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.
如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.