题目内容
一个多边形的内角和是1980°，则它的边数是 ，它的外角和是 ．
考点：多边形内角与外角
专题：
分析：根据多边形内角和定理：（n-2）×180°，列方程解答出即可求得边数，然后根据多边形的外角和定理求得外角和．
解答：解：根据多边形内角和定理得，
（n-2）×180°=1980°，
解得，n=13．
外角和是360°．
故答案是：13，360°．
（n-2）×180°=1980°，
解得，n=13．
外角和是360°．
故答案是：13，360°．
点评：本题考查了多边形的内角和定理和外角和定理，熟记公式是正确解答的基础．
练习册系列答案
名师点拨卷系列答案
英才计划期末调研系列答案
相关题目
在直角三角形ABC中，∠ACB=90°，CE为高，AF为角平分线，黄河农场各用10块面积相同的试验田种植甲、乙两种麦子，收获后对两种麦子产量（单位：吨/亩）的数据统计如下：
甲=0.61，
乙=0.59，S甲2=0.01，S乙2=0.002，则由上述数据推断乙种麦子产量比较稳定的依据是（ ）
. |
| x |
. |
| x |
A、
| ||||
| B、S甲2＞S乙2 | ||||
C、
| ||||
D、
|
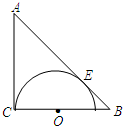已知：如图，△ABC是等腰直角三角形，∠C=90°，AC=BC=1，在BC上取一点O，以O为圆心，OC为半径作半圆与AB相切于点E．
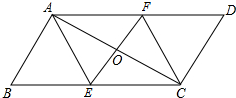如图，平行四边形ABCD中，E、F分别为BC、AD的中点．连接EF交AC于O，连接AB、FC．
如图，在△ABC中，∠BAC＜90°，AB=AC，AF⊥BC于点F，D为CA延长线上一点，DE⊥BC于E，交AB边于点G，则图中与∠D相等的角的个数为（ ）