题目内容
张老师为了从平时在班级里数学成绩比较优秀的王军、张成两位同学中选拔一人参加“全国初中数学联赛”,对两位同学进行了辅导,并在辅导期间进行了10次测试,两位同学测试成绩记录如下:
王军10次成绩分别是:68 80 78 79 81 77 78 84 83 92;
张成10次成绩分别是:86 80 75 83 85 77 79 80 80 75.
利用提供的数据,解答下列问题:
(1)填写完成下表:
(2)张老师从测试成绩记录表中,求得王军10次测试成绩的方差S王2=33.2,请你帮助张老师计算张成10次测试成绩的方差;
(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
王军10次成绩分别是:68 80 78 79 81 77 78 84 83 92;
张成10次成绩分别是:86 80 75 83 85 77 79 80 80 75.
利用提供的数据,解答下列问题:
(1)填写完成下表:
| 平均成绩 | 中位数 | 众数 | |
| 王军 | 80 | 79.5 | |
| 张成 | 80 | 80 |
(3)请你根据上面的信息,运用所学的统计知识,帮助张老师做出选择,并简要说明理由.
考点:方差,加权平均数,中位数,众数
专题:
分析:(1)根据众数的定义可得王军成绩的众数为78,再把张成10次成绩由小到大排列,然后利用中位数的定义求张成成绩的中位数;、
(2)先把张成的成绩都减去80得-5-5-3-1 0 0 0 3 5 6,然后根据方差的定义计算这组数据的方差,即可得到张成10次测试成绩的方差;
(3)在平均数相同的情况下,利用中位数、众数和方差的意义进行判断.
(2)先把张成的成绩都减去80得-5-5-3-1 0 0 0 3 5 6,然后根据方差的定义计算这组数据的方差,即可得到张成10次测试成绩的方差;
(3)在平均数相同的情况下,利用中位数、众数和方差的意义进行判断.
解答:解:(1)王军成绩的众数为78,
张成10次成绩由小到大排列为:75 75 77 79 80 80 80 83 85 86,
所以张成的中位数为80;
故答案为78,80;
(2)把张成的成绩都减去80得-5-5-3-1 0 0 0 3 5 6,
新数据的平均数为0,
所以这组数据的方差S2=
[2×(-5-0)2+(-3-0)2+(-1-0)2+3×(0-0)2+(3-0)2+(5-0)2+(6-0)2]=13
即张成10次测试成绩的方差为13;
(3)张老师应该选择张成去.因为他们的平均数相同,而张成成绩的众数和中位数都比王军的要大,且张成10次成绩的方差较小,也就是说他的成绩波动小,所以应该选择他去.
张成10次成绩由小到大排列为:75 75 77 79 80 80 80 83 85 86,
所以张成的中位数为80;
故答案为78,80;
(2)把张成的成绩都减去80得-5-5-3-1 0 0 0 3 5 6,
新数据的平均数为0,
所以这组数据的方差S2=
| 1 |
| 10 |
即张成10次测试成绩的方差为13;
(3)张老师应该选择张成去.因为他们的平均数相同,而张成成绩的众数和中位数都比王军的要大,且张成10次成绩的方差较小,也就是说他的成绩波动小,所以应该选择他去.
点评:本题考查了方差:一般地设n个数据,x1,x2,…xn的平均数为
,则方差S2=
[(x1-
)2+(x2-
)2+…+(xn-
)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.
. |
| x |
| 1 |
| n |
. |
| x |
. |
| x |
. |
| x |

练习册系列答案
相关题目
设有12只型号相同的杯子,其中一等品7只,二等品3只,三等品2只.则从中任意取1只,是二等品的概率等于( )
A、
| ||
B、
| ||
C、
| ||
| D、1 |
 在直角三角形ABC中,∠ACB=90°,CE为高,AF为角平分线,
在直角三角形ABC中,∠ACB=90°,CE为高,AF为角平分线,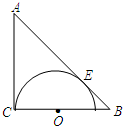 已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.
已知:如图,△ABC是等腰直角三角形,∠C=90°,AC=BC=1,在BC上取一点O,以O为圆心,OC为半径作半圆与AB相切于点E.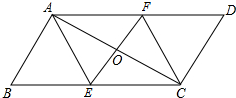 如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.
如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.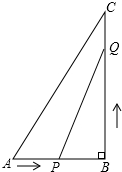 如图所示,在Rt△ABC中,∠B=90°,AB=18cm,BC=36cm,一点P从A沿AB边以2cm/s的速度向B点移动;点Q从B点开始沿BC边以6cm/s的速度向C点移动.如果P、Q两点同时出发,求几秒后Rt△BPQ的面积等于Rt△ABC的面积的
如图所示,在Rt△ABC中,∠B=90°,AB=18cm,BC=36cm,一点P从A沿AB边以2cm/s的速度向B点移动;点Q从B点开始沿BC边以6cm/s的速度向C点移动.如果P、Q两点同时出发,求几秒后Rt△BPQ的面积等于Rt△ABC的面积的 如图,在△ABC中,∠BAC<90°,AB=AC,AF⊥BC于点F,D为CA延长线上一点,DE⊥BC于E,交AB边于点G,则图中与∠D相等的角的个数为( )
如图,在△ABC中,∠BAC<90°,AB=AC,AF⊥BC于点F,D为CA延长线上一点,DE⊥BC于E,交AB边于点G,则图中与∠D相等的角的个数为( )