题目内容
 如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E,交AC于点F.求证:2AD=PE+PF.
如图,在△ABC中,AB=AC,AD⊥BC于点D,点P在BC上,PE⊥BC,交BA的延长线于点E,交AC于点F.求证:2AD=PE+PF.考点:等腰三角形的判定与性质,矩形的判定与性质
专题:证明题
分析:证明BD=CD;证明△ABD∽△EBP,△CPF∽△CDA,列出比例式,相加即可解决问题.
解答: 证明:∵AB=AC,AD⊥BC,
证明:∵AB=AC,AD⊥BC,
∴BD=CD;而PE⊥BC,
∴AD∥PE;
∴△ABD∽△EBP,△CPF∽△CDA;
∴
=
,
=
,
∴
=
,而PB+PC=2BD,
∴2AD=PE+PF.
 证明:∵AB=AC,AD⊥BC,
证明:∵AB=AC,AD⊥BC,∴BD=CD;而PE⊥BC,
∴AD∥PE;
∴△ABD∽△EBP,△CPF∽△CDA;
∴
| PE |
| AD |
| PB |
| BD |
| PF |
| AD |
| PC |
| DC |
∴
| PE+PF |
| AD |
| PB+PC |
| BD |
∴2AD=PE+PF.
点评:该题以等腰三角形为载体,在考查等腰三角形的性质的同时,还渗透了对相似三角形的判定及其性质等几何知识点的考查;对综合的分析问题解决问题的能力提出了一定的要求.

练习册系列答案
相关题目
老师给出:a+b=2,a2+b2=2,你能计算出ab的值为( )
| A、0 | ||
B、-
| ||
| C、-1 | ||
| D、1 |
某工程需在规定日期内完成,若甲工程队独做,恰好如期完成,如果乙工程队独做,则超过规定日期3天完成,现在甲、乙两队合作2天,剩下的由乙队独做,恰好在规定日期完成,求规定日期,如果设规定日期为x天,则下列正确( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
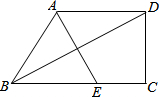 如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是
如图,梯形ABCD中,AD∥BC,∠C=90°,且AB=AD,连结BD,过A点作BD的垂线,交BC于E.如果EC=3cm,CD=4cm,那么,梯形ABCD的周长是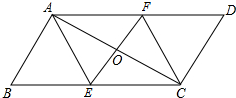 如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.
如图,平行四边形ABCD中,E、F分别为BC、AD的中点.连接EF交AC于O,连接AB、FC.