题目内容
14.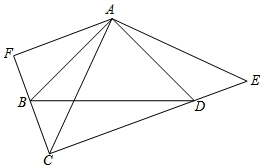 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.(1)若AC=10,求四边形ABCD的面积;
(2)求证:CE=2AF.
分析 (1)求出∠BAC=∠EAD,根据SAS推出△ABC≌△ADE,推出四边形ABCD的面积=三角形ACE的面积,即可得出答案;
(2)过点A作AG⊥CG,垂足为点G,求出AF=AG,求出CG=AG=GE,即可得出答案.
解答 解:
(1)∵∠BAD=∠CAE=90°,
∴∠BAC+∠CAD=∠EAD+∠CAD
∴∠BAC=∠EAD,
在△ABC和△ADE中,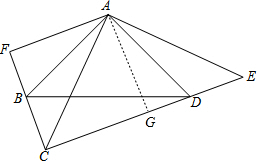
$\left\{\begin{array}{l}{AB=AD}\\{∠BAC=∠DAE}\\{AC=AE}\end{array}\right.$,
∴△ABC≌△ADE(SAS),
∵S四边形ABCD=S△ABC+S△ACD,
∴S四边形ABCD=S△ADE+S△ACD=S△ACE=$\frac{1}{2}$×102=50;
(2)证明:∵△ACE是等腰直角三角形,
∴∠ACE=∠AEC=45°,
由△ABC≌△ADE得:
∠ACB=∠AEC=45°,
∴∠ACB=∠ACE,
∴AC平分∠ECF;
过点A作AG⊥CG,垂足为点G,
∵AC平分∠ECF,AF⊥CB,
∴AF=AG,
又∵AC=AE,
∴∠CAG=∠EAG=45°,
∴∠CAG=∠EAG=∠ACE=∠AEC=45°,
∴CG=AG=GE,
∴CE=2AG,
∴CE=2AF.
点评 本题考查了全等三角形的性质和判定,等腰三角形的性质和判定,角平分线性质,直角三角形的性质的应用,能综合运用性质进行推理是解此题的关键,难度适中.

练习册系列答案
相关题目
4.正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A,B,C,D把原正方形分割成一些三角形(互相不重叠):

(1)填写表:
(2)若用y表示内部有n个点时正方形ABCD被分割成的三角形的个数,试写出y=2(n+1)(用含有n的代数式表示,n是正整数);
(3)正方形ABCD能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.

(1)填写表:
| 正方形ABCD内点的个数 | 1 | 2 | 3 | 4 | … |
| 分割成的三角形的个数 | 4 | 6 | 8 | 10 | … |
(3)正方形ABCD能否被分割成2016个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
6.根据国家发改委实施“阶梯电价”的有关文件要求,某市结合地方实际,决定从2015年5月1日起对居民生活用电试行“阶梯电价”收费,具体收费标准见表:
若2015年5月份,该市居民甲用电100度,交电费60元.
(1)上表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价为每度0.62元?
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度但不超过300度的部分 | 0.65 |
| 超过300度的部分 | 0.9 |
(1)上表中,a=0.6;若居民乙用电200度,则应交电费122.5元;
(2)若某用户某月用电量超过300度,设用电量为x度,请你用含x的代数式表示应交的电费;
(3)试行“阶梯电价”收费以后,该市一户居民月用电多少度时,其当月的平均电价为每度0.62元?
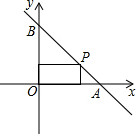 已知一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点.
已知一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点.
 如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.
如图,直线OC、BC的函数关系式分别是y1=x和y2=-2x+6,动点P(x,0)在OB上运动(0<x<3),过点P作直线m与x轴垂直.