题目内容
5.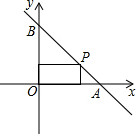 已知一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点.
已知一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点.(1)求a,b的值;
(2)在线段AB上任取一点P(x,y),过点P分别作x轴与y轴的垂线段,垂足分别为M,N,求矩形OMPN的面积S,并求出S的最大值.
分析 (1)因为一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点,根据待定系数法可求a,b的值;
(2)因为四边形OMPN是矩形,点P在直线y=-x+3上,PN=t,所以P(t,-t+3),即PM=-t+3,而S=PN•PM,由此即可得到S与t的函数关系式,再配方可求S的最大值.
解答 解:(1)∵一次函数y=ax+b(a≠0)的图象经过A(3,0),B(0,3)两点,
∴$\left\{\begin{array}{l}{3a+b=0}\\{b=3}\end{array}\right.$,
∴解得$\left\{\begin{array}{l}{a=-1}\\{b=3}\end{array}\right.$.
(2)∵四边形OMPN是矩形,
∵PN⊥y轴,PM⊥x轴,
∵点P在直线y=-x+3上,PN=t,
∴P(t,-t+3),
∴PM=-t+3,
∴S=t(-t+3)=-(t-1.5)2+2.25,
故S的最大值是2.25.
点评 此题考查了二次函数的应用,一次函数图象上点的坐标特征,解决本题这类问题常用到分类讨论、数形结合、方程和转化等数学思想方法.

练习册系列答案
相关题目
15.若点M(-3,2)和点N(a,b)关于y轴对称,则$\frac{b}{a}$的值为( )
| A. | $\frac{2}{3}$ | B. | $\frac{3}{2}$ | C. | -$\frac{2}{3}$ | D. | -$\frac{3}{2}$ |
 如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.
如图,在矩形ABCD中,AB=3,AD=4,若以点A为圆心,以4为半径作⊙A,则点A,点B,点C,点D四点中在⊙A外的是C.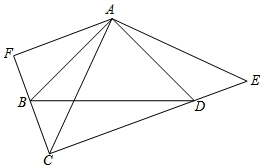 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.