题目内容
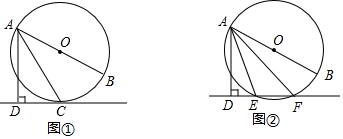
19.已知直线l与⊙O,AB是⊙O的直径,AD⊥l于点D.(1)如图①,当直线l与⊙O相切于点C时,若∠DAC=30°,求∠BAC的大小;
(2)如图②,当直线l与⊙O相交于点E,F时,若∠DAE=18°,求∠BAF的大小.
分析 (1)连接OD,易证OC∥AD,所以∠OCA=∠DAC,由因为OA=OC,所以∠OAC=∠OCA;
(2)连接BE,AB是⊙O的直径,所以∠AEB=90°,从而可知∠BEF=∠DAE=18°,由圆周角定理可知:∠BAF=∠BEF=18°
解答 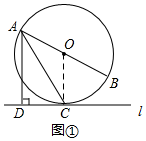 解:(1)连接OC、
解:(1)连接OC、
∵l是⊙O的切线,
∴OC⊥l,
∵AD⊥l,
∴OC∥AD,
∴∠OCA=∠DAC=30°,
∵OA=OC,
∴∠OAC=∠OCA=30°,
(2)连接BE,
∵AB是⊙O的直径,
∴∠AEB=90°,
∴∠AED+∠BEF=90°,
∵∠AED+∠DAE=90°,
∴∠BEF=∠DAE=18°,
∵$\widehat{BF}=\widehat{BF}$,
∴∠BAF=∠BEF=18°
点评 本题考查圆的综合问题,涉及切线的性质,圆周角定理等知识,题目较为综合.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目
7.已知一组正数a,b,c,d的平均数为2,则a+2,b+2,c+2,d+2的平均数为( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
11.已知$\frac{1}{x}$-$\frac{1}{y}$=5,则分式$\frac{2x+3xy-2y}{x-2xy-y}$的值为( )
| A. | 1 | B. | 5 | C. | $\frac{13}{7}$ | D. | $\frac{13}{3}$ |
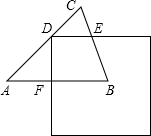 如图,在△ABC中,AB=AC=1,∠A=60°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y.
如图,在△ABC中,AB=AC=1,∠A=60°,边长为1的正方形的一个顶点D在边AC上,与△ABC另两边分别交于点E、F,DE∥AB,将正方形平移,使点D保持在AC上(D不与A重合),设AF=x,正方形与△ABC重叠部分的面积为y. 如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.
如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CF,垂足为F.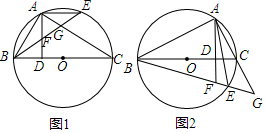
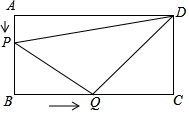 如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).
如图所示,在长方形ABCD中,AB=6厘米,BC=12厘米,点P沿AB边从点A开始向点B以1厘米/秒的速度移动,点Q沿BC从点B开始向点C以2厘米/秒的速度移动,如果P、Q同时出发,用t(秒)表示移动的时间(0≤t≤6).