题目内容
10. 如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于点O,AO的延长线交BC于F,求证:AF垂直平分BC.
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于点O,AO的延长线交BC于F,求证:AF垂直平分BC.
分析 通过△ABD≌△ACE,于是得到AE=AD,通过Rt△AEO≌Rt△ADO,证得∠BAF=∠CAF,根据等腰三角形的性质即可得到结论.
解答 证明:∵BD⊥AC于D,CE⊥AB于E,
∴∠AEC=∠ADB=90°,
在△ABD与△AEC中,$\left\{\begin{array}{l}{∠ADB=∠AEC}\\{∠BAC=∠BAC}\\{AB=AC}\end{array}\right.$,
∴△ABD≌△ACE,
∴AE=AD,
在Rt△AEO与Rt△ADO中,$\left\{\begin{array}{l}{AD=AE}\\{AO=AO}\end{array}\right.$,
∴Rt△AEO≌Rt△ADO,
∴∠BAF=∠CAF,
∵AB=AC,
∴AF垂直平分BC.
点评 本题考查了等腰三角形的性质,线段垂直平分线的判定,全等三角形的判定和性质,熟练掌握各定理是解题的关键.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
18.“!”是一种运算符号,并且1!=1,2!=1×2,3!=1×2×3,4!=1×2×3×4,…,则$\frac{2012!}{2011!}$的值为( )
| A. | 2009 | B. | 2010 | C. | 2011 | D. | 2012 |
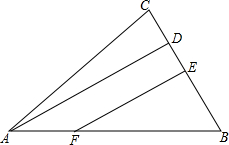 已知:如图,AD⊥BC于D,E为BC中点,EF⊥BC交AB于F,AB=9cm,BC=6cm,DC=2cm,求AF的长.
已知:如图,AD⊥BC于D,E为BC中点,EF⊥BC交AB于F,AB=9cm,BC=6cm,DC=2cm,求AF的长. 如图所示,AB=AC=AD,请说明:
如图所示,AB=AC=AD,请说明: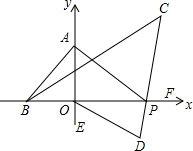 如图,在平面直角坐标系中,∠ABO=2∠BAO,P为x轴正半轴一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE
如图,在平面直角坐标系中,∠ABO=2∠BAO,P为x轴正半轴一动点,BC平分∠ABP,PC平分∠APF,OD平分∠POE 如图,以直线x=-1为对称轴的二次函数y=ax2+bx+c经过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a-2b+c>0;④若(-5,y1)($\frac{5}{2}$,y2)是该二次函数图象上的两个点,则y1>y2.其中说法正确的是①②④.(只填序号)
如图,以直线x=-1为对称轴的二次函数y=ax2+bx+c经过点(-3,0),下列说法:①abc<0;②2a-b=0;③4a-2b+c>0;④若(-5,y1)($\frac{5}{2}$,y2)是该二次函数图象上的两个点,则y1>y2.其中说法正确的是①②④.(只填序号)