题目内容
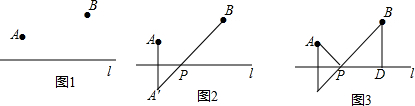
7.请阅读下列材料:问题:如图1,点A,B在直线l的同侧,在直线l上找一点P,使得AP+BP的值最小.小明的思路是:如图2,作点A关于直线l的对称点A',连接A'B,则A'B与直线l的交点P即为所求.
请你参考小明同学的思路,探究并解决下列问题:
(1)如图3,在图2的基础上,设AA'与直线l的交点为C,过点B作BD⊥l,垂足为D.若CP=1,PD=2,AC=1,写出AP+BP的值为3$\sqrt{2}$;
(2)将(1)中的条件“AC=1”去掉,换成“BD=4-AC”,其它条件不变,写出此时AP+BP的值5;
(3)$\sqrt{{{(2m-3)}^2}+1}$+$\sqrt{{{(8-2m)}^2}+4}$的最小值为$\sqrt{34}$.
分析 (1)利用勾股定理求得PA,根据三角形相似对应边成比例求得PB,从而求得PA+PB;
(2)作AE∥l,交BD的延长线于E,根据已知条件求得BE、A′E,然后根据勾股定理即可求得A′B,从而求得AP+BP的值;
(3)设AC=2m-3,PC=1,则PA=$\sqrt{(2m-3)^{2}+1}$;设BD=8-2m,PD=2,则PB=$\sqrt{{{(8-2m)}^2}+4}$,结合(2)即可求得.
解答  解:(1)如图2,∵AA′⊥l,AC=1,PC=1,
解:(1)如图2,∵AA′⊥l,AC=1,PC=1,
∴PA=$\sqrt{2}$,
∴PA′=PA=$\sqrt{2}$,
∵AA′∥BD,
∴∠A′=∠B,
∵∠A′PC=∠BPD,
∴△A′PC∽△BPD,
∴$\frac{PB}{PA′}$=$\frac{PD}{PC}$,
∴$\frac{PB}{\sqrt{2}}$=$\frac{2}{1}$,
∴PB=2$\sqrt{2}$,
∴AP+PB=$\sqrt{2}$+2$\sqrt{2}$=3$\sqrt{2}$;
故答案为3$\sqrt{2}$;
(2)作AE∥l,交BD的延长线于E,如图3,
则四边形A′EDC是矩形,
∴AE=DC=PC+PD=3,DE=A′C=AC,
∵BD=4-AC,
∴BD+AC=BD+DE=4,
即BE=4,
在RT△A′BE中,A′B=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AP+BP=5,
故答案为5;
(3)如图3,设AC=2m-3,PC=1,则PA=$\sqrt{(2m-3)^{2}+1}$;设BD=8-2m,PD=2,则PB=$\sqrt{{{(8-2m)}^2}+4}$,
∵DE=AC=2m-3,
∴BE=BD+DE=5,A′E=CD=PC+PD=3
∴PA+PB=A′B=$\sqrt{A′{E}^{2}+B{E}^{2}}$=$\sqrt{{5}^{2}+{3}^{2}}$=$\sqrt{34}$.
故答案为$\sqrt{34}$.
点评 本题考查了轴对称-最短路线问题,熟练掌握轴对称的性质和勾股定理的应用是解题的关键.

 阅读快车系列答案
阅读快车系列答案| A. | m=$\frac{2}{3}$ | B. | m=$\frac{2}{3}$或m=2 | C. | m=$\frac{1}{2}$ | D. | m=$\frac{2}{3}$或m=$\frac{1}{2}$ |
| A. | x<-$\frac{3}{4}$ | B. | x>-$\frac{3}{4}$ | C. | x>$\frac{3}{4}$ | D. | x<$\frac{3}{4}$ |
| A. | a-3<b-3 | B. | $\frac{a}{5}$<$\frac{b}{5}$ | C. | -3a>-3b | D. | 3-2a<3-2b |
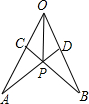 如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )
如图,在∠AOB的两边上截取AO=BO,OC=OD,连接AD,BC交于点P,连接OP,则图中全等三角形共有( )| A. | 5对 | B. | 4对 | C. | 3对 | D. | 2对 |
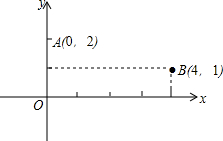 已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.
已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.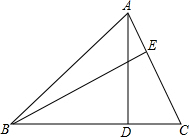 如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE=$\frac{24}{5}$cm.
如图,AD,BE分别是△ABC的高,AD=4,BC=6,AC=5,则BE=$\frac{24}{5}$cm. 已知,∠α
已知,∠α