题目内容
17.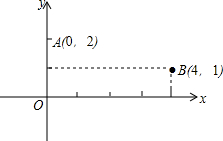 已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.
已知两点A(0,2),B(4,1),点P是x轴上的点,且PA+PB的值最小,求点P的坐标.
分析 先求得直线BC的解析式,然后利用一次函数与坐标轴交点求法得出答案即可.
解答 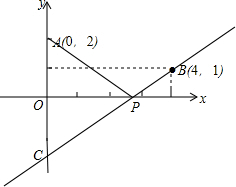 解:∵A(0,2),
解:∵A(0,2),
∴A点关于x轴对称点C坐标为;(0,-2),
连接A′B交x轴于点P,
由题意得;A′(0,-2),
将A′(0,-2),B(4,1)代入y=kx+b得:$\left\{\begin{array}{l}{b=-2}\\{4k+b=1}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=\frac{3}{4}}\\{b=-2}\end{array}\right.$,
∴直线A′B的解析式为:y=$\frac{3}{4}$x-2,
∴y=0时,x=$\frac{8}{3}$,
∴P($\frac{8}{3}$,0).
点评 此题主要考查了最短路径求法以及待定系数法求一次函数解析式等知识,求得直线BC的解析式是解题关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
20.下列二次根式中的最简二次根式是( )
| A. | $\sqrt{{x}^{2}}$ | B. | $\frac{x}{\sqrt{3}}$ | C. | $\sqrt{8}$ | D. | $\frac{\sqrt{2x}}{2}$ |
9.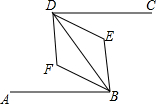 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
 如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )
如图,已知AB∥DC,BF平分∠ABE,且BF∥DE,则∠ABE与∠CDE的关系是( )| A. | ∠ABE=2∠CDE | B. | ∠ABE=3∠CDE | C. | ∠ABE=∠CDE+90° | D. | ∠ABE+∠CDE=180° |
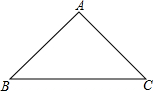 在△ABC中,AB=AC,∠BAC=90°,若点D、E在边BC上,∠DAE=45°,BE=CD=4,求AC的长.
在△ABC中,AB=AC,∠BAC=90°,若点D、E在边BC上,∠DAE=45°,BE=CD=4,求AC的长.
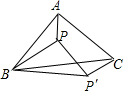 如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合.
如图,在△ABC中,BA=BC,∠ABC=45°,P是△ABC内一点,△ABP旋转后能与△CBP′重合. 如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF=3cm.
如图,在Rt△ABC中,∠ACB=90°,D、E、F分别是AB、BC、CA的中点,若CD=3cm,则EF=3cm.