题目内容
3.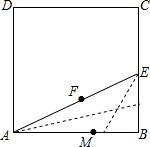 欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )
欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )| A. | 线段BB″ | B. | 线段AB″ | C. | 线段BE | D. | 线段AE |
分析 设AB″=AB′=x,则AE=x+$\frac{1}{2}$,在Rt△ABE中利用勾股定理得到($\frac{1}{2}$)2+12=(x+$\frac{1}{2}$)2,整理得到x2+x-1=0,则根据一元二次方程根的定义可判断线段AB′或AB″是方程x2+x-1=0的一个正根.
解答 解: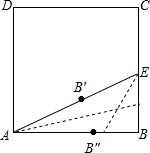 设AB″=x,则AB′=x,
设AB″=x,则AB′=x,
∵EB′=EB=$\frac{1}{2}$,
∴AE=x+$\frac{1}{2}$,
在Rt△ABE中,∵BE2+AB2=AE2,
∴($\frac{1}{2}$)2+12=(x+$\frac{1}{2}$)2,
∴x2+x-1=0,
∴线段AB′或AB″是方程x2+x-1=0的一个正根.
故选B.
点评 本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了一元二次方程根的定义和勾股定理.

练习册系列答案
 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
11.表1给出了正比例函数y=kx的图象上部分点的坐标,表2给出了反比例函数y=$\frac{m}{x}$的图象上部分点的坐标,则当kx=$\frac{m}{x}$时,x的值为±2.
表1
表2
表1
| x | 0.5 | 1 | 2 | 4 |
| y | -0.25 | -0.5 | -1 | -2 |
| x | 0.5 | 1 | 2 | 4 |
| y2 | -4 | -2 | -1 | -0.5 |
18. 如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )
如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )
 如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )
如图,在5×5的正方形网格中,线段AB的长度与下列哪个整数最接近( )| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
20.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表:
(1)表中反映了哪些变量之间的关系?哪个是自变量?哪个是因变量?
(2)当物体的质量为3kg时,弹簧的长度为多少?
(3)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(4)当物体的质量为2.5kg时,根据(3)的关系式,求弹簧的长度.
| 物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | 5 |
| 弹簧的长度(cm) | 12 | 12.5 | 13 | 13.5 | 14 | 14.5 |
(2)当物体的质量为3kg时,弹簧的长度为多少?
(3)如果物体的质量为xkg,弹簧的长度为ycm,根据上表写出y与x的关系式;
(4)当物体的质量为2.5kg时,根据(3)的关系式,求弹簧的长度.
 如图,?ABCD的周长为80,AB边上的高线DE=$\frac{1}{2}$AD,设AB=x,?ABCD的面积为y,求y关于x的函数表达式及自变量x的取值范围.
如图,?ABCD的周长为80,AB边上的高线DE=$\frac{1}{2}$AD,设AB=x,?ABCD的面积为y,求y关于x的函数表达式及自变量x的取值范围.