题目内容
12. 如图,?ABCD的周长为80,AB边上的高线DE=$\frac{1}{2}$AD,设AB=x,?ABCD的面积为y,求y关于x的函数表达式及自变量x的取值范围.
如图,?ABCD的周长为80,AB边上的高线DE=$\frac{1}{2}$AD,设AB=x,?ABCD的面积为y,求y关于x的函数表达式及自变量x的取值范围.
分析 利用平行四边的周长可表示出AD=40-x,则0<x<40;然后根据平行四边形的面积公式即可得到y(cm2)与x的函数关系式.
解答 解:∵?ABCD的周长为80,
∴AD+AB=40,
∵AB=x,
∴AD=40-x,
∵DE=$\frac{1}{2}$AD,
∴DE=20-$\frac{1}{2}$x,
∴y=DE×AB=x(20-$\frac{1}{2}$x)=-$\frac{1}{2}$x2+20x(0<x<40).
点评 此题主要考查了平行四边形的性质以及根据实际问题列二次函数解析式,正确表示出DE的长是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.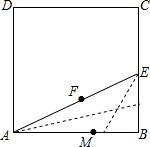 欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )
欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )
 欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )
欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )| A. | 线段BB″ | B. | 线段AB″ | C. | 线段BE | D. | 线段AE |
9.某电器超市销售每台进价分别200元、170元的A、B两种型号的电风扇,下表是近两周的销售情况:
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 3台 | 5台 | 1800元 |
| 第一周 | 4台 | 10台 | 3100元 |
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元,不少于5340元的金额再采购这两种型号的电风扇共30台,求A、B两种型号的电风扇的采购方案;
(3)在(2)的条件下,超市销售完这30台电风扇,用所获利润再次购进A/B两种型号的电风扇且恰好全部售出,请直接写出再次销售的A、B两种型号的电风扇各多少台所获最大利润?最大利润是多少?
 在如图所示的平面直角坐标系中,将坐标是(1,0),(0,4),(2,4),(4,4),(3,0),的点用线段依次连接起来形成一个图案.
在如图所示的平面直角坐标系中,将坐标是(1,0),(0,4),(2,4),(4,4),(3,0),的点用线段依次连接起来形成一个图案.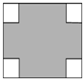 如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.
如图所示,在一个边长为12cm的正方形的四个角都剪去一个大小相等的小正方形,当小正方形的边长由小到大变化时,图中阴影部分的面积也随之发生变化.