题目内容
13.已知一次函数图象过($\frac{\sqrt{3}}{2}$,1),且和x轴相交成30°的角,求此解析式.分析 由于直线和x轴相交成30°的角,则可设直线解析式为y=-$\frac{\sqrt{3}}{3}$x+b,然后把已知点的坐标代入求出对应的b的值即可.
解答 解:设直线解析式为y=kx+b,
因为直线和x轴相交成30°的角,
所以k=±$\frac{\sqrt{3}}{3}$,
把($\frac{\sqrt{3}}{2}$,1)代入y=-$\frac{\sqrt{3}}{3}$x+b得-$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$+b=1,解得b=$\frac{3}{2}$;
把($\frac{\sqrt{3}}{2}$,1)代入y=$\frac{\sqrt{3}}{3}$x+b得$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$+b=1,解得b=$\frac{1}{2}$;
所以直线解析式为y=-$\frac{\sqrt{3}}{3}$x+$\frac{3}{2}$或y=$\frac{\sqrt{3}}{3}$x+$\frac{1}{2}$.
点评 本题考查了定系数法求一次函数解析式:(1)先设出函数的一般形式,如求一次函数的解析式时,先设y=kx+b;(2)将自变量x的值及与它对应的函数值y的值代入所设的解析式,得到关于待定系数的方程或方程组;(3)解方程或方程组,求出待定系数的值,进而写出函数解析式.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
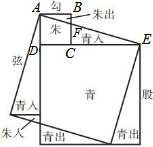 魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中BF=1,CF=2,则AE的长为3$\sqrt{10}$.
魏朝时期,刘徽利用下图通过“以盈补虚,出入相补”的方法,即“勾自乘为朱方,股自乘为青方,令出入相补,各从其类”证明了勾股定理.若图中BF=1,CF=2,则AE的长为3$\sqrt{10}$. 如图,正方形网格中,每个小正方形的边长为1,△ABC的顶点在格点上,则△ABC中,边长是无理数的边有2条.
如图,正方形网格中,每个小正方形的边长为1,△ABC的顶点在格点上,则△ABC中,边长是无理数的边有2条.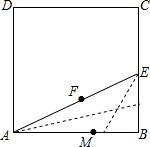 欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )
欧几里得在《几何原本》中,记载了用图解法解方程x2+ax=b2的方法,类似地可以用折纸的方法求方程x2+x-1=0的一个正根.如图,裁一张边长为1的正方形的纸片ABCD,先折出BC的中点E,再折出线段AE,然后通过折叠使EB落在线段EA上,折出点B的新位置B′,因而EB′=EB,类似地,在AB上折出点B″使AB″=AB′,表示方程x2+x-1=0的一个正根的线段是( )