题目内容
10.已知:二次函数y=ax2+bx+c,y与x的一些对应值如表:| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| ax2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当1<x≤4时,y的取值范围是-1≤y≤3.

分析 (1)把表中三组对应值代入y=ax2+bx+c中得关于a、b、c的方程组,然后解方程组求出a、b、c即可得到抛物线解析式,然后计算自变量为-1、1、3所对应的函数值;
(2)先把解析式配成顶点式,然后利用描点法画函数图象,再利用函数图象写出1<x≤4时所对应y的取值范围.
解答 解:(1)将点(0,3)、(2,-1)、(4,3)代入y=ax2+bx+c中,
$\left\{\begin{array}{l}{c=3}\\{4a+2b+c=-1}\\{16a+4b+c=3}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=-4}\\{c=3}\end{array}\right.$,
∴二次函数的解析式为y=x2-4x+3.
当x=-1时,y=8;当x=1时,y=0;当x=3时,y=0.
(2)如图,y=x2-4x+3=(x-2)2-1,抛物线的顶点坐标为(2,-1),
当1<x≤4时,y的取值范围是-1≤y≤3.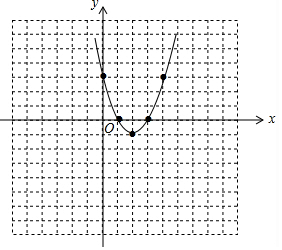
故答案为:8,0,0;y=x2-4x+3;-1≤y≤3.
点评 本题考查了用待定系数法求二次函数的解析式:在利用待定系数法求二次函数关系式时,要根据题目给定的条件,选择恰当的方法设出关系式,从而代入数值求解.一般地,当已知抛物线上三点时,常选择一般式,用待定系数法列三元一次方程组来求解;当已知抛物线的顶点或对称轴时,常设其解析式为顶点式来求解;当已知抛物线与x轴有两个交点时,可选择设其解析式为交点式来求解.

练习册系列答案
相关题目
20.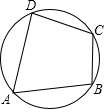 如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )
如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )
 如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )
如图,四边形ABCD是⊙O的内接四边形.若∠A:∠B:∠C=1:2:4,则∠D为( )| A. | 90° | B. | 100° | C. | 108° | D. | 144° |
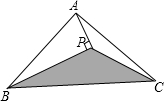 如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是$\frac{1}{2}$cm2.
如图所示,三角形ABC的面积为1cm2.AP垂直∠B的平分线BP于点P.则三角形PBC的面积是$\frac{1}{2}$cm2.
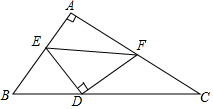 如图,△ABC中,∠A=90°,AB=3,AC=4,点D是BC上的动点,E、F分别在AB、AC上,∠EDF=90°,若以D、E、F为顶点的三角形与△ABC相似,则BD=$\frac{9}{5}$或$\frac{5}{2}$.
如图,△ABC中,∠A=90°,AB=3,AC=4,点D是BC上的动点,E、F分别在AB、AC上,∠EDF=90°,若以D、E、F为顶点的三角形与△ABC相似,则BD=$\frac{9}{5}$或$\frac{5}{2}$.