题目内容
20．
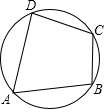如图，四边形ABCD是⊙O的内接四边形．若∠A：∠B：∠C=1：2：4，则∠D为（ ）| A． | 90° | B． | 100° | C． | 108° | D． | 144° |
分析 根据圆内接四边形的性质得∠A+∠C=180°，∠B+∠D=180°，则利用∠A：∠B：∠C=1：2：4可计算出∠A和∠B，然后利用互补计算出∠D．
解答 解：∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠C=180°，∠B+∠D=180°，
∵∠A：∠B：∠C=1：2：4，
∴∠A=$\frac{1}{5}$×180°=36°，
∴∠B=2∠A=72°，
∴∠D+180°-∠B=180°-72°=108°．
故选C．
点评 本题考查了圆内接四边形的性质：圆内接四边形的对角互补；圆内接四边形的任意一个外角等于它的内对角．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
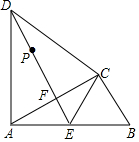如图，在△ABC中，∠ACB=90°，以AC为底边作等腰三角形△ACD，AD=CD，E为AB的中点，连接CE、DE，DE与AC相交于点F．
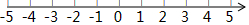结合数轴与绝对值的知识回答下列问题：
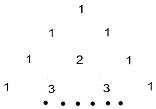如图，为杨辉三角的一部分，它的作用是指导读者按规律写出形如（a+b）n （n为正整数）展开式的系数，请你仔细观察下列等式中的规律，利用杨辉三角解决下列问题．
10．已知：二次函数y=ax2+bx+c，y与x的一些对应值如表：
（1）根据表格中的数据，确定二次函数解析式为y=x2-4x+3；
（2）填齐表格中空白处的对应值并利用表，用五点作图法，画出二次函数y=ax2+bx+c的图象．（不必重新列表）
（3）当1＜x≤4时，y的取值范围是-1≤y≤3．
| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| ax2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
（2）填齐表格中空白处的对应值并利用表，用五点作图法，画出二次函数y=ax2+bx+c的图象．（不必重新列表）
（3）当1＜x≤4时，y的取值范围是-1≤y≤3．