题目内容
19.已知抛物线y=ax2经过点(2,-3),则a=-$\frac{3}{4}$,其对称轴是y轴,并且在对称轴左侧,y随x的增大而增大.分析 把已知点的坐标代入可求得a的值,由解析式可求得其对称轴,再结合开口方向和增减性可求得答案.
解答 解:
∵抛物线y=ax2经过点(2,-3),
∴-3=22×a,解得a=-$\frac{3}{4}$,
∴y=-$\frac{3}{4}$x2,
∴抛物线开口向下,对称轴为y轴,
当x<0时,y随x的增大而增大,
∴在对称轴左侧,y随x的增大而增大,
故答案为:-$\frac{3}{4}$;y轴;左.
点评 本题主要考查二次函数的性质,掌握函数图象上的点的坐标满足函数解析式是解题的关键.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
10.已知:二次函数y=ax2+bx+c,y与x的一些对应值如表:
(1)根据表格中的数据,确定二次函数解析式为y=x2-4x+3;
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当1<x≤4时,y的取值范围是-1≤y≤3.

| x | … | -1 | 0 | 1 | 2 | 3 | 4 | … |
| ax2+bx+c | … | 8 | 3 | 0 | -1 | 0 | 3 | … |
(2)填齐表格中空白处的对应值并利用表,用五点作图法,画出二次函数y=ax2+bx+c的图象.(不必重新列表)
(3)当1<x≤4时,y的取值范围是-1≤y≤3.

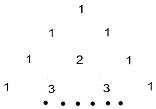 如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如(a+b)n (n为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.
如图,为杨辉三角的一部分,它的作用是指导读者按规律写出形如(a+b)n (n为正整数)展开式的系数,请你仔细观察下列等式中的规律,利用杨辉三角解决下列问题.

 如图,菱形ABCD的边BC在x轴上,点A,D在第一象限,线段AB交y轴于E,且E为AB的中点,点M为AC和BD的交点,连接CE,有CE⊥AB,点A的坐标为(1,2$\sqrt{3}$);
如图,菱形ABCD的边BC在x轴上,点A,D在第一象限,线段AB交y轴于E,且E为AB的中点,点M为AC和BD的交点,连接CE,有CE⊥AB,点A的坐标为(1,2$\sqrt{3}$); 如图,AB是⊙O的直径,C是半圆O上的一点,CD切⊙O于C,AD⊥CD,垂足为D,AD交⊙O于E,若E是$\widehat{AC}$的中点,⊙O的半径为1,则图中阴影部分的面积为$\frac{\sqrt{3}}{8}$.
如图,AB是⊙O的直径,C是半圆O上的一点,CD切⊙O于C,AD⊥CD,垂足为D,AD交⊙O于E,若E是$\widehat{AC}$的中点,⊙O的半径为1,则图中阴影部分的面积为$\frac{\sqrt{3}}{8}$. 如图,在等边△ABC中,AB=2,D、E为BC、AC上两动点,BD=CE,AD、BE相交于M点,求CM的最小值为$\frac{2\sqrt{3}}{3}$.
如图,在等边△ABC中,AB=2,D、E为BC、AC上两动点,BD=CE,AD、BE相交于M点,求CM的最小值为$\frac{2\sqrt{3}}{3}$.