题目内容
 如图,梯形ABCD中,AD∥BC,AC⊥BD于O,试判断AB+CD与AD+BC的大小,并证明你的结论.
如图,梯形ABCD中,AD∥BC,AC⊥BD于O,试判断AB+CD与AD+BC的大小,并证明你的结论.考点:梯形,三角形三边关系,三角形中位线定理
专题:证明题
分析:作梯形ABCD的中位线EF,连接OE、OF,根据梯形中位线定理得出EF=
(AD+BC),根据直角三角形斜边上中线定理得出OE=
AB,OF=
CD,在△OEF中根据三角形三边关系定理得出OE+OF>EF,代入即可求出AB+CD>AD+BC.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:作梯形ABCD的中位线EF,连接OE、OF,
即EF=
(AD+BC),
∵AC⊥BD,
∵∠AOB=∠DOC=90°,
∵E为AB中点,F为DC中点,
∴OE=
AB,OF=
CD,
∵在△OEF中,OE+OF>EF,
∴
AB+
CD>
(AD+BC),
∴AB+CD>AD+BC,
∴AD+BC<AB+CD.
即EF=
| 1 |
| 2 |
∵AC⊥BD,
∵∠AOB=∠DOC=90°,

∵E为AB中点,F为DC中点,
∴OE=
| 1 |
| 2 |
| 1 |
| 2 |
∵在△OEF中,OE+OF>EF,
∴
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴AB+CD>AD+BC,
∴AD+BC<AB+CD.
点评:此题的难点在于将所求的线段转换到同一个三角形中,而正确地作出辅助线是顺利解题的前提;题目综合了梯形的中位线,三角形的三边关系定理,直角三角形斜边上中线定理等重要知识点,难度较大.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
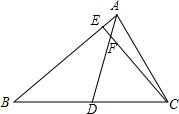 如图,△ABC中,AD是BC边上的中线,F是AD上一点,有AF:FD=1:5,连接CF,并延长交AB于E,则AE:EB等于( )
如图,△ABC中,AD是BC边上的中线,F是AD上一点,有AF:FD=1:5,连接CF,并延长交AB于E,则AE:EB等于( )| A、1:6 | B、1:8 |
| C、1:9 | D、1:10 |
 变与不变将一长方形纸片折出如图所示的图形,其中∠AEB=30°,BG:GH:HC=2:4:1,如果DH=3cm,求AE+EF的长.
变与不变将一长方形纸片折出如图所示的图形,其中∠AEB=30°,BG:GH:HC=2:4:1,如果DH=3cm,求AE+EF的长. 如图已知点B、D分别在∠A的两边上,C为∠A内一点,且AB=AD,CD=BC,CE⊥AD于E,CF⊥AB于F.试判断CE与CF是否相等,并说明理由.
如图已知点B、D分别在∠A的两边上,C为∠A内一点,且AB=AD,CD=BC,CE⊥AD于E,CF⊥AB于F.试判断CE与CF是否相等,并说明理由. 如图,长方形ABCD正好被分成6个正方形,如果中间最小的正方形面积等于1,那么长方形ABCD的面积等于
如图,长方形ABCD正好被分成6个正方形,如果中间最小的正方形面积等于1,那么长方形ABCD的面积等于