题目内容
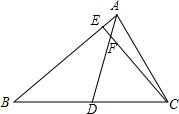如图，△ABC中，AD是BC边上的中线，F是AD上一点，有AF：FD=1：5，连接CF，并延长交AB于E，则AE：EB等于（ ）| A、1：6 | B、1：8 |
| C、1：9 | D、1：10 |
考点：三角形的角平分线、中线和高,平行线分线段成比例
专题：计算题
分析：过点D作EC的平行线，得到BE的中点G，再用平行线分线段成比例定理得到AE：EG=AF：FD，然后求出AE：EB的值．
解答：
解：如图：过点D作DG∥EC交AB于G，
∵AD是BC边上的中线，∴BD=CD，∴BG=GE．
∵DG∥EC，∴AE：EG=AF：FD=1：5．
∴AE：EB=1：10．
故选D．
解：如图：过点D作DG∥EC交AB于G，∵AD是BC边上的中线，∴BD=CD，∴BG=GE．
∵DG∥EC，∴AE：EG=AF：FD=1：5．
∴AE：EB=1：10．
故选D．
点评：本题考查的是相似三角形的判定和性质，根据题目告诉AF：FD的值，可以过点D作EC的平行线，得到BE的中点，再根据平行线分线段成比例定理得到AE：EG=AF：FD，可以求出AE：EB的值．
练习册系列答案
阅读快车系列答案
相关题目
如图，梯形ABCD中，AD∥BC，AC⊥BD于O，试判断AB+CD与AD+BC的大小，并证明你的结论．
为了庆祝国庆，学校准备在教学楼大厅的圆柱体柱子上贴彩带，已知柱子的底面周长为lm，高为3m．如果要求彩带从柱子底端的A处绕柱子4圈后到达柱子顶端的B处，那么至少应购买彩带用10根长度相同的木棍拼成一个三角形（不剩余木棍也不折断木棍），则只能拼成（ ）
| A、直角三角形 |
| B、等腰三角形 |
| C、等腰直角三角形 |
| D、等边三角形 |
已知：m2+m-1=0，那么代数式m3+2m2-1997的值是（ ）
| A、1997 | B、-1997 |
| C、1996 | D、-1996 |